在一个无限大均匀带电平面附近 用绝缘丝线悬挂一电量为q 质量为m的小球。设丝线的质量可忽略 小球上的
在一个无限大均匀带电平面附近，用绝缘丝线悬挂一电量为q、质量为m的小球。设丝线的质量可忽略，小球上的电荷不影响带电平面的电荷分布。小球处于平衡状态时，丝线的张角为θ，如图14-6（a）所示。求带电平面的面电荷密度。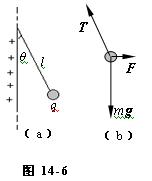 
请帮忙给出正确答案和分析，谢谢！
参考解答
481***100
2024-11-03 03:14:46
正确答案：对小球做受力分析可知小球受重力、丝线的张力和带电平面的静电力作用如图14-6（b）所示。因小球处于平衡状态故小球所受合力为零。设无限大均匀带电平面的面电荷密度为σ。则其在小球所在处产生的电场强度的大小为E=σ/(2ε0)小球受到的静电力为F=qE=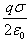
（1）根据牛顿第二定律分别列出水平方向和竖直方向的力平衡方程得到F-Tsinθ=0 （2）Tcosθ-mg=0 （3）联立求解式（2）和（3）得到F=mgtanθ （4）联立求解式（1）和（4）得到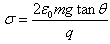 
对小球做受力分析可知,小球受重力、丝线的张力和带电平面的静电力作用,如图14-6（b）所示。因小球处于平衡状态,故小球所受合力为零。设无限大均匀带电平面的面电荷密度为σ。则其在小球所在处产生的电场强度的大小为E=σ/(2ε0),小球受到的静电力为F=qE=（1）根据牛顿第二定律分别列出水平方向和竖直方向的力平衡方程,得到F-Tsinθ=0（2）Tcosθ-mg=0（3）联立求解式（2）和（3）,得到F=mgtanθ（4）联立求解式（1）和（4）,得到
相似问题
一对同轴无限长空心直导体圆筒 内 外半径分别为R和R2（筒壁厚度可以忽略）。电流I沿内筒流去 沿外筒
一对同轴无限长空心直导体圆筒，内、外半径分别为R和R2（筒壁厚度可以忽略）。电流I沿内筒流去，沿外筒流回，如图17-6所示。求：（1）两筒间的磁感应强度
如图14-7所示 电场强度分量分别为Ex=bx1/2 Ey=Ez=0 其中b=800N.C-1 图中
如图14-7所示，电场强度分量分别为Ex=bx1 2，Ey=Ez=0，其中b=800N C-1，图中a=10cm。试求通过立方体的电通量。 请帮忙给出正确答案和分析，谢谢！
有一个电容为40μF 与阻值为60Ω的电阻串联后接在电压为220V 频率为50Hz的交流电源上 求：
有一个电容为40μF，与阻值为60Ω的电阻串联后接在电压为220V，频率为50Hz的交流电源上，求：（1）阻抗Z；（2）功率因数cosψ；（3）有功功率；（4）无功
一只平板电容器的电容为C 充有电量Q 并已经与电源断开．用力将电介质从电容器中拉出 其他不变．这一过
一只平板电容器的电容为C，充有电量Q，并已经与电源断开．用力将电介质从电容器中拉出，其他不变．这一过程外力做功为A．试求电介质的相对介电常量．请帮
一个带电量为q（q>0）的均匀带电细线 弯成半径为R 带有缺口的圆环。缺口的长度为d（d
一个带电量为q（q>0）的均匀带电细线，弯成半径为R、带有缺口的圆环。缺口的长度为d（d<<R）。求圆心处的电场强度。请帮忙给出正确答案和分析，谢谢！
