光纤芯的折射率为n1 包层的折射率为n2 光纤所在介质的折射率为n0 求光纤的数值孔径NA(即n0s
光纤芯的折射率为n1，包层的折射率为n2，光纤所在介质的折射率为n0，求光纤的数值孔径NA(即n0sinI0，其中I0为光在光纤内能以全反射方式传播时在入射端面的最大人射角)。
请帮忙给出正确答案和分析，谢谢！
参考解答
481***102
2024-11-19 09:14:26
正确答案：光纤内的全反射现象如图1．7所示。位于光纤入射端面满足由空气入射到光纤芯中应用折射定律则有 n0sinI0=n1sinI0' (1—2) 而当光束由光纤芯入射到包层时满足全反射使得光束可以在光纤内传播则有
由式(1—2)和式(1—3)联立可得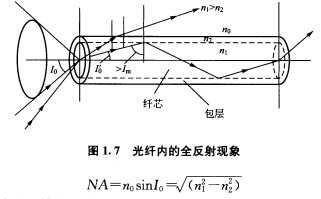
光纤内的全反射现象如图1．7所示。位于光纤入射端面,满足由空气入射到光纤芯中,应用折射定律则有n0sinI0=n1sinI0'(1—2)而当光束由光纤芯入射到包层时满足全反射,使得光束可以在光纤内传播,则有由式(1—2)和式(1—3)联立可得
相似问题
设f(t)=δ(t—t0) 则[f(t)]=( )．A．1B．2πC．D．请帮忙给出正确答案和分析
设f(t)=δ(t—t0)，则[f(t)]=( )．A．1B．2πC．D．请帮忙给出正确答案和分析，谢谢！
求函数f(t)=e-βt(β>0 t≥0)的Fourier正弦积分和余弦积分表达式．请帮忙给出正确答
求函数f(t)=e-βt(β>0，t≥0)的Fourier正弦积分和余弦积分表达式．请帮忙给出正确答案和分析，谢谢！
证明：以下的M1与M2都是n次对称群Sn的生成系． 1)所有含1的对换：M1={(12) (13)
证明：以下的M1与M2都是n次对称群Sn的生成系． 1)所有含1的对换：M1={(12)，(13)，…．(1n)}： 2)M2={(12)，(12…n)} (n＞2)．请帮忙给出正确答案和分析，谢谢！
求下列二次曲面的奇点 并说明二次曲面是否退化? (1)χ22－χ42－2χ1χ3－2χ2χ4＝0；
求下列二次曲面的奇点，并说明二次曲面是否退化? (1)χ22－χ42－2χ1χ3－2χ2χ4＝0； (2)； (3)aχ12＋bχ22－cχ32＝0，(abc≠0)； (4)χ22－χ3
求矩形脉冲函数求函数f(t)=e－t(t≤0)的Fourier正弦变换 并推证求函数f(t)=e-t
求矩形脉冲函数求函数f(t)=e－t(t≤0)的Fourier正弦变换，并推证求函数f(t)=e-t(t≤0)的Fourier正弦变换，并推证 请帮忙给出正确答案和分析，谢谢！
