假设矩阵A和B满足关系式AB＝A＋2B 其中已知矩阵且矩阵X满足 AXA＋BXB＝AXB＋BXA＋

大学本科已帮助：人时间:2024-11-16 09:11:33

假设矩阵A和B满足关系式AB＝A＋2B，其中已知矩阵，且矩阵X满足 AXA＋BXB＝AXB＋BXA＋E，其中E为3阶
已知矩阵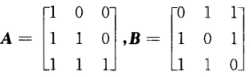
，且矩阵X满足 AXA＋BXB＝AXB＋BXA＋E，其中E为3阶单位矩阵，求X。
请帮忙给出正确答案和分析，谢谢！

481***102

2024-11-16 09:11:33



正确答案：由题设关系式有 AX(A—B)＋BX(B—A)＝E。即 (A—B)X(A—B)＝E．由于行列式｜A—B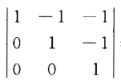｜＝≠0所以矩阵A—B可逆而 (A—B)^－1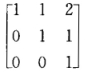＝故 x＝[(A—B)^－1²＝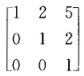
本题是解矩阵方程的问题，其一般步骤是先化简，再计算．

设A为m×N矩阵 C是n阶可逆矩阵矩阵A的秩为r 矩阵B＝AC的秩为r1 则A．r＞r1．B．r＜

设A为m×N矩阵，C是n阶可逆矩阵，矩阵A的秩为r，矩阵B＝AC的秩为r1，则A．r＞r1．B．r＜r1．C．r＝r1．D．r与r1的关系依C而定．请帮忙给出正确答案和分析，谢谢！
设4阶方阵A＝则A的逆矩阵A－1＝_______．请帮忙给出正确答案和分析谢谢！

设4阶方阵A＝，则A的逆矩阵A－1＝_______．请帮忙给出正确答案和分析，谢谢！
已知函数f(x y)在点(0 0)的某个领域内连续且则( )．A．点(0 0)是 (x y)的极大

已知函数f(x，y)在点(0，0)的某个领域内连续，且则( )．A．点(0，0)是，(x，y)的极大值点B．点(0，0)是f(x，y)的极小值点C．点(0，0)不是f(x，y)的极值
求m n 使1m25n4897为偶排列．请帮忙给出正确答案和分析谢谢！

求m，n，使1m25n4897为偶排列．请帮忙给出正确答案和分析，谢谢！
某项新技术要在总数为N个的企业群体中推广 p(t)为t时刻已掌握该项技术的企业数设新技术推广方式一

某项新技术要在总数为N个的企业群体中推广，p(t)为t时刻已掌握该项技术的企业数，设新技术推广方式一方面采用已掌握该项技术的企业逐渐向尚未推广该项技

设A为m×N矩阵 C是n阶可逆矩阵矩阵A的秩为r 矩阵B＝AC的秩为r1 则A．r＞r1．B．r＜