一颗质量为m的珠子系在线的一端 线的另一端固定在天花板上 线长为l0先拉动珠子使线保持水平静止 然后
一颗质量为m的珠子系在线的一端，线的另一端固定在天花板上，线长为l0先拉动珠子使线保持水平静止，然后松手使珠子下落。求摆下角度q时这个珠子的速率和线的张力。
请帮忙给出正确答案和分析，谢谢！
参考解答
473***100
2024-11-04 10:09:40
正确答案：以珠子为研究对象则当珠子在下落过程的任意位置时对其做受力分析如图2-6所示。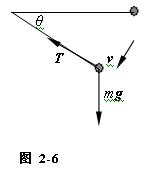
根据牛顿运动定律分别列出沿切线和法线方向的方程有
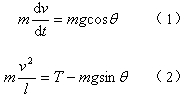整理式（1）做变量代换有
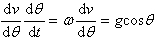（3）将上式两端同乘以绳长l就有v=lω。根据初始条件对式（3）做积分有∫0vvdv=∫0qglcosθdθ （4）完成积分求解可得珠子的速率为
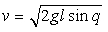由式（2）可解得线中的张力为T=mgsinq+
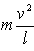=mgsinq+2mgsinq=3mgsinq
以珠子为研究对象,则当珠子在下落过程的任意位置时,对其做受力分析如图2-6所示。根据牛顿运动定律,分别列出沿切线和法线方向的方程,有整理式（1）,做变量代换有（3）将上式两端同乘以绳长l,就有v=lω。根据初始条件,对式（3）做积分有∫0vvdv=∫0qglcosθdθ（4）完成积分,求解可得珠子的速率为由式（2）可解得线中的张力为T=mgsinq+=mgsinq+2mgsinq=3mgsinq
相似问题
已知某质点的运动学方程为x=5+2t—2t2 单位为SI制．求： (1)质点在第2s内通过的位移；
已知某质点的运动学方程为x=5+2t—2t2，单位为SI制．求： (1)质点在第2s内通过的位移； (2)该质点在第0．3s和第1s末的速度和加速度； (3)问质点做什么
质量m=4.0kg的雪橇 沿与水平面夹角θ=36.9°的斜坡向下滑动 所受空气阻力与速度成正比 比例
质量m=4 0kg的雪橇，沿与水平面夹角θ=36 9°的斜坡向下滑动，所受空气阻力与速度成正比，比例系数k未知。今测得雪橇运动的速率—时间关系如图2-9所示。t
一个升降机内地板上放有物体A 其上再放另一物体B 二者的质量分别为MA MB．当升降机以加速度a向下
一个升降机内地板上放有物体A，其上再放另一物体B，二者的质量分别为MA、MB．当升降机以加速度a向下加速运动时(a＜g)，物体A对升降机地板的压力在数值上
用离心泵将敞口水池中的水送往一敞口高位槽 高位槽液面高出水池液面5 m．管径为50 mm。当泵出口管
用离心泵将敞口水池中的水送往一敞口高位槽，高位槽液面高出水池液面5 m．管径为50 mm。当泵出口管路中阀门全开(ζ=0．17)时，泵入口管中真空表读数为5
离心泵的特性曲线He-qv与管路的特性曲线H-qv有何不同?两者的交点意味着什么?请帮忙给出正确答案
离心泵的特性曲线He-qv与管路的特性曲线H-qv有何不同?两者的交点意味着什么?请帮忙给出正确答案和分析，谢谢！
