某大学数学测验 抽得20个学生的分数平均数 样本方差s2=16 假设分数服从正态分布 求σ2的置信度
某大学数学测验，抽得20个学生的分数平均数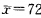
，样本方差s2=16，假设分数服从正态分布，求σ2的置信度为98％的置信区间．
请帮忙给出正确答案和分析，谢谢！
参考解答
473***101
2024-11-12 07:41:36
正确答案：由题意知应取χ2分布变量构造成1一a的σ2的置信区间为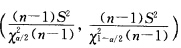
已知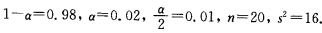
查χ2分布表是χ0.012(19)=36．191χ0.992(19)=7．633于是得σ2的98％的置信区间为
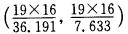即(8．40039．827)．
由题意知,应取χ2分布变量,构造成1一a的σ2的置信区间为已知查χ2分布表是χ0.012(19)=36．191,χ0.992(19)=7．633,于是得σ2的98％的置信区间为即(8．400,39．827)．
相似问题
设随机变量X的分布函数为且已知试求a b的值．请帮忙给出正确答案和分析 谢谢！
设随机变量X的分布函数为且已知试求a，b的值．请帮忙给出正确答案和分析，谢谢！
设f(x1 x2 … xn)=XTAX是一实二次型 λ1 λ2 … λn是A的特征值 且λ1≤λ2≤
设f(x1，x2，…，xn)=XTAX是一实二次型，λ1，λ2，…，λn是A的特征值，且λ1≤λ2≤…≤λn证明：对设A，B是两个n阶实设A，B是两个n阶实对称矩阵，且B
设f(x1 x2 … xn)=XTAX是一实二次型 λ1 λ2 … λn是A的特征值 且λ1≤λ2≤
设f(x1，x2，…，xn)=XTAX是一实二次型，λ1，λ2，…，λn是A的特征值，且λ1≤λ2≤…≤λn证明：对设A∈Cn×n，x，y∈Cn，设A∈Cn×n，x，y∈Cn，(x，
设随机变量X的分布函数为任选三个月 求至少有一个月营业额大于2c的概率．任选三个月 求至少有一个月营
设随机变量X的分布函数为任选三个月，求至少有一个月营业额大于2c的概率．任选三个月，求至少有一个月营业额大于2c的概率．请帮忙给出正确答案和分析，谢谢！
设f(x1 x2 … xn)=XTAX是一实二次型 λ1 λ2 … λn是A的特征值 且λ1≤λ2≤
设f(x1，x2，…，xn)=XTAX是一实二次型，λ1，λ2，…，λn是A的特征值，且λ1≤λ2≤…≤λn证明：对设A∈Cm×n是正交投设A∈Cm×n是正交投影，则A的特
