设F(x＋z y＋z)可微分 求由方程F(x＋z y＋z)－1／2(x2＋y2＋z2)＝2确定的函数
设F(x＋z，y＋z)可微分，求由方程F(x＋z，y＋z)－1／2(x2＋y2＋z2)＝2确定的函数z＝z(x．y)的微分出与偏导数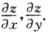
请帮忙给出正确答案和分析，谢谢！
参考解答
473***101
2024-11-08 09:31:22
正确答案：对F(x＋zy＋z)－1／2(x2＋y2＋z2)＝2两边微分得dF－1／2(dx2＋dy2＋dz2)＝0 Fˊ1d(x＋z)＋Fˊ2(y＋z)－1／2(2xdx＋2ydy＋2zdz)＝0(Fˊ1－x)dx＋(fˊ2－y)dy＋(Fˊ1＋Fˊ2－z)dz＝0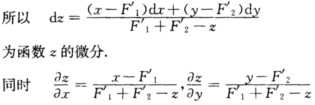
对F(x＋z,y＋z)－1／2(x2＋y2＋z2)＝2两边微分得dF－1／2(dx2＋dy2＋dz2)＝0Fˊ1d(x＋z)＋Fˊ2(y＋z)－1／2(2xdx＋2ydy＋2zdz)＝0(Fˊ1－x)dx＋(fˊ2－y)dy＋(Fˊ1＋Fˊ2－z)dz＝0
相似问题
求曲线x2＋z2＝10 y2＋z2＝10在点(1 1 3)处的切线和法平面方程．请帮忙给出正确答案和
求曲线x2＋z2＝10，y2＋z2＝10在点(1，1，3)处的切线和法平面方程．请帮忙给出正确答案和分析，谢谢！
设u＝f(x y z)有连续的一阶偏导数 又函数y＝y(x)及z＝z(x)分别由下列两式确定：exy
设u＝f(x，y，z)有连续的一阶偏导数，又函数y＝y(x)及z＝z(x)分别由下列两式确定：exy－xy＝2和请帮忙给出正确答案和分析，谢谢！
设圆锥体的底半径R 由 30 cm增加到30．1 cm 高H由60 cm减少到55 cm 试求圆锥体
设圆锥体的底半径R 由 30 cm增加到30．1 cm，高H由60 cm减少到55 cm，试求圆锥体体积变化的近似值．请帮忙给出正确答案和分析，谢谢！
求二元函数z＝f(x y)＝x2y(4－x－y)在直线x＋y＝6 x轴和y轴所围成的闭区域D上的最大
求二元函数z＝f(x，y)＝x2y(4－x－y)在直线x＋y＝6，x轴和y轴所围成的闭区域D上的最大值和最小值．请帮忙给出正确答案和分析，谢谢！
利用三重积分计算下列立体Ω的体积： (1)Ω＝｛(x y z)｜ a＞0 b＞0 c＞0｝； (2)
利用三重积分计算下列立体Ω的体积： (1)Ω＝｛(x，y，z)｜，a＞0，b＞0，c＞0｝； (2)Ω＝｛(x，y，z)｜x2＋z2≤1，｜x｜＋｜y｜≤1｝； (3)Ω＝｛(x
