设同一平面内的四点a(a1 a2 a3) b(b1 b2 b3) c(c1 c2 c3) d(d1

正确答案：令ad二点连线与bC二点连线的交点为t(t₁、t₂、t₃)如图2—2—21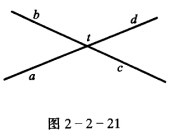． 则由定理3．4得 d_i＝pa_i＋qt_i (i＝123) 其中p≠0q≠0同理得 t_i＝rb_i＋sc_i (i＝123) 其中r≠0s≠0因此得 d_i＝pa_i＋q(rb_i＋sc_i) d_i＝pa_i＋qrb_i＋qsc_i (i＝123) 令pa_i＝a′_iqrb_i＝b′_iqsc_i＝c′_i－d_i＝d′_i 则得a′_i＋b′_i＋c′_i＋d′_i＝0 (i＝123)
令a,d二点连线与b,C二点连线的交点为t(t1、t2、t3),如图2—2—21．则由定理3．4得di＝pai＋qti(i＝1,2,3)其中p≠0,q≠0,同理得ti＝rbi＋sci(i＝1,2,3)其中r≠0,s≠0,因此得di＝pai＋q(rbi＋sci)di＝pai＋qrbi＋qsci(i＝1,2,3)令pai＝a′i,qrbi＝b′,iqsci＝c′i,－di＝d′i,则得a′i＋b′i＋c′i＋d′i＝0(i＝1,2,3)