将下列函数按勒让德多项式展开： (1)f(x)=x3 (2)f(x)=|x| 求表面充电至电位为v0

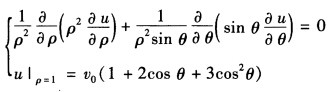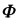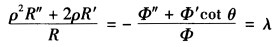正确答案：由定解问题及条件的形式可知所求调和函数u只与变量ρθ有关故所给定解问题为利用变量分离法令u(ρθ=R(ρ).(θ)有令λ=ι(ι+1)则上式化为两个常微分方程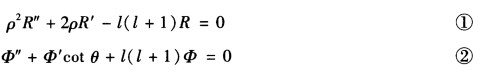由物理意义可知函数u(ρθ)有界则R(ρ)(θ)分别是有界函数由勒让德方程②可得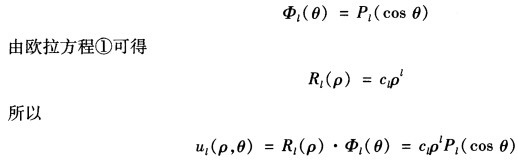由叠加原理得原问题的解为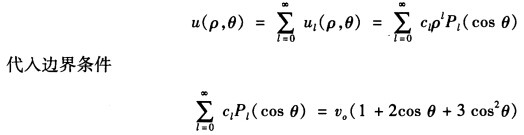c₀=2v₀c₁=2v₀c₂=2vc_ι=0(ι≥3)则 u(ρθ)=2v₀[P₀(cos θ)+P₁(cos θ).ρ+P₂(cos θ)ρ²
由定解问题及条件的形式可知,所求调和函数u只与变量ρ,θ有关,故所给定解问题为利用变量分离法,令u(ρ,θ=R(ρ).(θ)有令λ=ι(ι+1),则上式化为两个常微分方程由物理意义可知,函数u(ρ,θ)有界,则R(ρ),(θ)分别是有界函数,由勒让德方程②可得由叠加原理得原问题的解为c0=2v0,c1=2v0,c2=2v,cι=0(ι≥3)则u(ρ,θ)=2v0[P0(cosθ)+P1(cosθ).ρ+P2(cosθ)ρ2