在半径为1的球内求解Laplace方程▽2u=0 使u|r=1=3cos2θ+1。请帮忙给出正确答案

正确答案：建立定解问题(使用球坐标)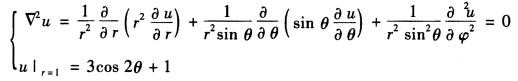：令u=u(rθφ)由于边界条件与φ无关知u与φ无关故u=u(rθ)=R(r)Θ(θ)代入方程分离变量并求解得 R_n(r)=A_nrⁿ+B_nr^-(n+1)n=012…于是问题解的形式为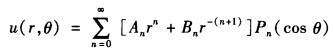由边界条件确定其中的常数。由式②得到B_n=0故球内问题的解为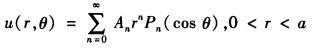由边界条件①得到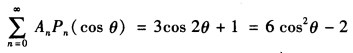由于等号的右边为cos θ的多项式因此可直接写成Legendre多项式的形式。因为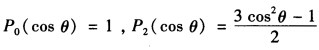所以 6 cos²θ-2=4P₂(cos θ)与左边A₀P₀(cos θ)+A_ι P_ι(cos θ)+A₂P₂(cos θ)+…比较得到 A₀=0A₁=0A₂=4A_n=0(n＞2)于是问题的解为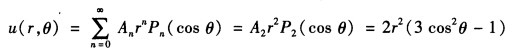
建立定解问题(使用球坐标)：令u=u(r,θ,φ),由于边界条件与φ无关,知u与φ无关,故u=u(r,θ)=R(r)Θ(θ)代入方程,分离变量并求解,得Rn(r)=Anrn+Bnr-(n+1),n=0,1,2,…于是问题解的形式为由边界条件确定其中的常数。由式②得到Bn=0,故球内问题的解为由边界条件①得到由于等号的右边为cosθ的多项式,因此可直接写成Legendre多项式的形式。因为所以6cos2θ-2=4P2(cosθ)与左边A0P0(cosθ)+AιPι(cosθ)+A2P2(cosθ)+…比较,得到A0=0,A1=0,A2=4,An=0(n＞2)于是问题的解为