一个n元实二次型可以分解成两个实系数1次齐次多项式的乘积当且仅当它的秩等于2 并且符号差为0 或者它

正确答案：必要性：设实系数二次型(x₁x₂…x_n)可以分解成两个实系数一次多项式的乘积f(x₁x₂…x_n)=(a₁x₁+a₂x₂+…+a_nx_n)(b₁x₁+b₂x₂+…+b_nx_n)如果向量(a₁a₂…a_n)与(b₁b₂…b_n)线性相关则它们成比例(b₁b₂…b_n)=k(a₁a₂…a_n)以(a₁a₂…a_n)为第一行作一个n阶可逆阵C则线性变换X=C^-1Y将(x₁x₂…x_n)化成f(x₁x₂…x_n)=ky₁²故f(x₁x₂…x_n)的秩为1．如果(a₁a₂…a_n)与(b₁b₂…b_n)线性无关．那么以它们前两行作一个n阶可逆矩阵C则线性替换X=C^-1Y将f(x₁x₂…x_n)化成f(x₁x₂…x_n)=y₁y₂再作一个可逆线性替换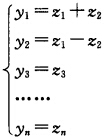则f(x₁x₂…x_n)化成规范形f(x₁x₂…x_n)=z₁²一z₂²所以f(x₁x₂…x_n)的秩为2符号差等于0．充分性f的秩为2符号差为0则可通过非奇异线性变换X=CY化为 f=y₁²一y₂²=(y₁+y₂)(y₁一y₂)由y=C^-1X即y₁y₂可由x₁x₂…x_n线性表示代入上式即知f是x₁x₂…x_n的两个一次齐式的乘积若的秩是1则f的规范形为y₁²根据同样道理知结论成立．
必要性：设实系数二次型,(x1,x2,…,xn)可以分解成两个实系数一次多项式的乘积f(x1,x2,…,xn)=(a1x1+a2x2+…+anxn)(b1x1+b2x2+…+bnxn)如果向量(a1,a2,…an)与(b1,b2,…,bn)线性相关,则它们成比例(b1,b2,…,bn)=k(a1,a2,…an)以(a1,a2,…an)为第一行作一个n阶可逆阵C,则线性变换X=C-1Y将,(x1,x2,…,xn)化成f(x1,x2,…,xn)=ky12,故f(x1,x2,…,xn)的秩为1．如果(a1,a2,…an)与(b1,b2,…,bn)线性无关．那么以它们前两行作一个n阶可逆矩阵C,则线性替换X=C-1Y将f(x1,x2,…,xn)化成f(x1,x2,…,xn)=y1y2再作一个可逆线性替换则f(x1,x2,…,xn)化成规范形f(x1,x2,…,xn)=z12一z22,所以f(x1,x2,…,xn)的秩为2,符号差等于0．充分性f的秩为2,符号差为0,则,可通过非奇异线性变换X=CY化为f=y12一y22=(y1+y2)(y1一y2)由y=C-1X,即y1,y2可由x1,x2,…,xn线性表示,代入上式,即知f是x1,x2,…,xn的两个一次齐式的乘积,若,的秩是1,则f的规范形为y12,根据同样道理知结论成立．