设实数域上的3级实对矩阵A为已知有特征值±1 问A能否对角化?说明理由．已知有特征值±1 问A能否对
设实数域上的3级实对矩阵A为已知有特征值±1，问A能否对角化?说明理由．
已知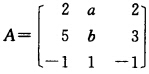
有特征值±1，问A能否对角化?说明理由．
请帮忙给出正确答案和分析，谢谢！
参考解答
490***101
2024-11-13 14:01:54
正确答案：由于λ1=1λ2=一1是A的特征值由此可知｜A一1I=｜A+I｜=0即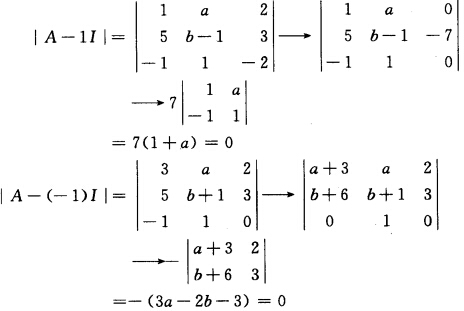
解得a=一1b=一3所以
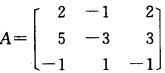根据λ1+λ2+λ3=α11+α22+α33得1+(一1)+λ3=2+(一3)+(一1)即λ3=一2由于A的3个特征值互异所以A可对角化．
由于λ1=1,λ2=一1是A的特征值,由此可知｜A一1I=｜A+I｜=0,即解得a=一1,b=一3,所以根据λ1+λ2+λ3=α11+α22+α33得1+(一1)+λ3=2+(一3)+(一1),即λ3=一2,由于A的3个特征值互异,所以A可对角化．
相似问题
若一个正态总体方差未知 检验H0：μ＝μ0 H1：μ≠μ0 抽取样本为(ξ1 ξ2 … ξn) 则拒
若一个正态总体方差未知，检验H0：μ＝μ0，H1：μ≠μ0，抽取样本为(ξ1，ξ2，…，ξn)，则拒绝域应与( )有关．A．样本值，显著性水平αB．样本值，显
函数f(x)＝2x3＋3x2—12x＋1在区间_________上为单调减函数．请帮忙给出正确答案和
函数f(x)＝2x3＋3x2—12x＋1在区间_________上为单调减函数．请帮忙给出正确答案和分析，谢谢！
函数y＝x—ln(1＋x2)的极值为( )．A．0B．1—ln 2C．—1—ln 2D．不存在此题为
函数y＝x—ln(1＋x2)的极值为( )．A．0B．1—ln 2C．—1—ln 2D．不存在此题为多项选择题。请帮忙给出正确答案和分析，谢谢！
在区间[0 8]上求曲线y＝x2的切线 使切线与y＝0和x＝8所围成的面积最大．请帮忙给出正确答案和
在区间[0，8]上求曲线y＝x2的切线，使切线与y＝0和x＝8所围成的面积最大．请帮忙给出正确答案和分析，谢谢！
以下各式中错误的是( )．A．f(x)dx＝0B．C．f'(x)dx＝f(b)—f(a)D．此题为多
以下各式中错误的是( )．A．f(x)dx＝0B．C．f "(x)dx＝f(b)—f(a)D．此题为多项选择题。请帮忙给出正确答案和分析，谢谢！
