求下列曲面所围成的立体在xOy面上的投影区域: (1)z=x2+y2与z=2-x2-y2; (2)
求下列曲面所围成的立体在xOy面上的投影区域: (1)z=x2+y2与z=2-x2-y2; (2)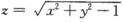 ,x2+y2=4与z=0.
,x2+y2=4与z=0.
请帮忙给出正确答案和分析,谢谢!
参考解答
正确答案:(1)在xOy面上的投影为Dxy={(xy)|x2+y2≤1};(2)在xOy面上的投影为Dxy={(xy)|x2+y2≤1}.
(1)在xOy面上的投影为Dxy={(x,y)|x2+y2≤1};(2)在xOy面上的投影为Dxy={(x,y)|x2+y2≤1}.
相似问题
设函数f(x y)可微 且对任意的x y 都有 则使不等式f(x1 y1)<f(x2 y1)成立的一
设函数f(x,y)可微,且对任意的x,y,都有,则使不等式f(x1,y1)<f(x2,y1)成立的一个充分条件是A.x1>x2,y1<y2.B.x1>x2,y1>y2.C.x1<x2,y1
设向量a={3 -4 2} 轴u的正向与三个坐标轴的正向构成相等的锐角 试求:(1)向量a在轴u上的
设向量a={3,-4,2},轴u的正向与三个坐标轴的正向构成相等的锐角,试求:(1)向量a在轴u上的投影;(2)向量a与轴u的夹角.请帮忙给出正确答案和分析,谢谢!
设u=f(x y z) ψ(x2 ey z)=0 y=sinx 其中f ψ都具有一阶连续偏导数 且.
设u=f(x,y,z),ψ(x2,ey,z)=0,y=sinx,其中f,ψ都具有一阶连续偏导数,且.请帮忙给出正确答案和分析,谢谢!
设有三元方程xy-zlny+exz=1 根据隐函数存在定理 存在点(0 1 1)的一个邻域 在此邻域
设有三元方程xy-zlny+exz=1,根据隐函数存在定理,存在点(0,1,1)的一个邻域,在此邻域内该方程A.只能确定一个具有连续偏导数的隐函数z=z(x,y).B
设f(u)具有二阶连续导数 且g(x y)=.请帮忙给出正确答案和分析 谢谢!
设f(u)具有二阶连续导数,且g(x,y)=.请帮忙给出正确答案和分析,谢谢!












