设函数z＝f(xy yg(x)) 函数f具有二阶连续偏导数 函数g(x)可导且在x＝1处取得极值g(
设函数z＝f(xy,yg(x))，函数f具有二阶连续偏导数，函数g(x)可导且在x＝1处取得极值g(1)＝1．求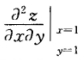
．
请帮忙给出正确答案和分析，谢谢！
参考解答
463***101
2024-11-08 19:12:14
正确答案：由题意g'(1)＝0． 因为
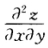＝f'1＋y[xf'11＋g(x)f'12＋g'(x)f'2＋yg'(x)[xf'21＋g(x)f'22所以令x＝y＝1且注意到g(1)＝1g'(1)＝0得
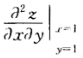＝f'1(11)＋f'11(1'1)＋f'12(11)．
利用多元复合函数的求偏导法则及g'(1)＝0．
相似问题
已知入射光线的路径为 求该光线经平面x＋2y＋5z＋17＝0的反射线方程．请帮忙给出正确答案和分析
已知入射光线的路径为，求该光线经平面x＋2y＋5z＋17＝0的反射线方程．请帮忙给出正确答案和分析，谢谢！
设z＝f(x y)是由方程z—y－x＋xez－y－x＝0所确定的二元函数 求dz．请帮忙给出正确答案
设z＝f(x，y)是由方程z—y－x＋xez－y－x＝0所确定的二元函数，求dz．请帮忙给出正确答案和分析，谢谢！
某厂家生产的一种产品同时在两个市场销售 售价分别为p1和p2；销售量分别为q1和q2；需求函数分别为
某厂家生产的一种产品同时在两个市场销售，售价分别为p1和p2；销售量分别为q1和q2；需求函数分别为 q2＝24－0．2p1，q2＝10－0．05p2 总成本函数为 C
求下列曲面所围成的立体在xOy面上的投影区域： (1)z＝x2＋y2与z＝2－x2－y2； (2)
求下列曲面所围成的立体在xOy面上的投影区域： (1)z＝x2＋y2与z＝2－x2－y2； (2)，x2＋y2＝4与z＝0．请帮忙给出正确答案和分析，谢谢！
设函数f(x y)可微 且对任意的x y 都有 则使不等式f(x1 y1)＜f(x2 y1)成立的一
设函数f(x，y)可微，且对任意的x，y，都有，则使不等式f(x1，y1)＜f(x2，y1)成立的一个充分条件是A．x1＞x2，y1＜y2．B．x1＞x2，y1＞y2．C．x1＜x2，y1
