某企业生产A B两种产品 它们都必须经过工序I和工序II。生产100件产品A在工序I上需要7小时 在
某企业生产A，B两种产品，它们都必须经过工序I和工序II。生产100件产品A在工序I上需要7小时，在工序II上需要4小时。生产100件产品B在工序I上需要6小时，在工序II上需要2小时。工序I有42小时，工序II有16小时能用于生产这两种产品。又生产100件产品A可实现利润5．50元，生产100件产品B可实现利润2元。为了获得最大利润，生产产品A和B各多少(假设所有的产品都可以销售出去)?
请帮忙给出正确答案和分析，谢谢！
参考解答
462***995
2024-10-30 07:07:50
正确答案：设生产产品A的数量为x(百件)B的数量为y(百件)。其约束条件为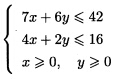
求x与y的值使得P=5．5x+2y达到最大值。画出可行解域K如图3．3所示。过(00)的等值线为5．5x+2y=0可见等值线5．5x+2y=P向右平行移动时P的值增加。在点(40)P=22即目标函数P=5．5x+2y在可行域K中取最大值22所以x=4y=0为最优解。即生产400件产品A和0件产品B时利润最大。
设生产产品A的数量为x(百件),B的数量为y(百件)。其约束条件为求x与y的值,使得P=5．5x+2y达到最大值。画出可行解域K,如图3．3所示。过(0,0)的等值线为5．5x+2y=0,可见,等值线5．5x+2y=P向右平行移动时,P的值增加。在点(4,0),P=22,即目标函数P=5．5x+2y在可行域K中取最大值22,所以x=4,y=0为最优解。即生产400件产品A和0件产品B时利润最大。
相似问题
检查图7．18是否为最优 若不是最优 将其调整为最优。 请帮忙给出正确答案和分析 谢谢！
检查图7．18是否为最优，若不是最优，将其调整为最优。 请帮忙给出正确答案和分析，谢谢！
对于氢原子和类氢离子的径向分布曲线D(r)一r图 下列叙述错误的是( )。A．径向峰数与节面数都与n
对于氢原子和类氢离子的径向分布曲线D(r)一r图，下列叙述错误的是( )。A．径向峰数与节面数都与n、l有关B．核周围电子出现的概率为0C．l相同时，n越大，
已知氢原子的一个波函数为∮＝A(r／a0)2sin2θsin2∮ 试求一电子处在该状态时的能量E 角
已知氢原子的一个波函数为∮＝A(r／a0)2sin2θsin2∮，试求一电子处在该状态时的能量E、角动量｜M｜以及角动量在磁场方向的分量。请帮忙给出正确答案和分析，谢谢！
掷两颗质地相同 形状均匀的骰子 骰子上的数字有1 2 3 4 5 6 出现点数的可能组合有62=36
掷两颗质地相同、形状均匀的骰子，骰子上的数字有1，2，3，4，5，6，出现点数的可能组合有62=36种，每个点数出现的机会都是相同的。请帮忙给出正确答案和
求类氢原子基态r的最可几值。请帮忙给出正确答案和分析 谢谢！
求类氢原子基态r的最可几值。请帮忙给出正确答案和分析，谢谢！
