设连续型随机变量X的概率密度为 求：(1)E(X)；(2)E(X2)；(3)E(2X+4X2)．请
设连续型随机变量X的概率密度为 
求：(1)E(X)；(2)E(X2)；(3)E(2X+4X2)．
请帮忙给出正确答案和分析，谢谢！
参考解答
460***444
2023-11-13 17:20:22
正确答案：(1)由(4．2)式及奇函数在对称区间上积分的性质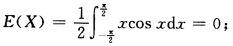
(2)由(4．4)式、偶函数在对称区间上积分的性质及分部积分法．
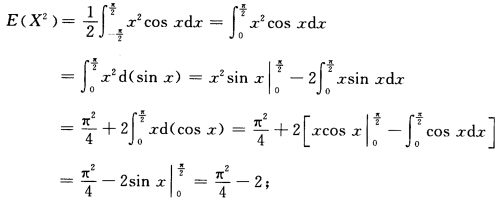(3)由数学期望的性质E(2X+4X2)=2E(X)+4E(X2)=π2—8．
(1)由(4．2)式及奇函数在对称区间上积分的性质,(2)由(4．4)式、偶函数在对称区间上积分的性质及分部积分法．(3)由数学期望的性质,E(2X+4X2)=2E(X)+4E(X2)=π2—8．
相似问题
设随机变量(X Y)的分布律为 求关于X和关于Y的边缘分布律 问X与Y是否独立?请帮忙给出正确答案
设随机变量(X，Y)的分布律为 求关于X和关于Y的边缘分布律，问X与Y是否独立?请帮忙给出正确答案和分析，谢谢！
设随机变量X与Y独立同分布 且概率密度为 求Z=XY的概率密度．请帮忙给出正确答案和分析 谢谢！
设随机变量X与Y独立同分布，且概率密度为 求Z=XY的概率密度．请帮忙给出正确答案和分析，谢谢！
设二维连续型随机变量(X Y)在区域D={(x y)：x2+y2≤1)上均匀分布 求X与Y的相关系数
设二维连续型随机变量(X，Y)在区域D={(x，y)：x2+y2≤1)上均匀分布，求X与Y的相关系数和(X，Y)的协方差矩阵．问X与Y是否不相关?是否独立?请帮忙给出正确
“三伐高丽”的是历史上哪一位皇帝?()A.汉武帝B.隋炀帝C.唐太宗D.明高宗
“三伐高丽”的是历史上哪一位皇帝?()A 汉武帝B 隋炀帝C 唐太宗D 明高宗
如X(t)=ξt+η定义的随机过程{X(t) t∈T}中 ξ η是同在区间[0 1]上均匀分布的相互
如X(t)=ξt+η定义的随机过程{X(t)，t∈T}中，ξ，η是同在区间[0，1]上均匀分布的相互独立的随机变量，试求其一维密度函数．请帮忙给出正确答案和分析，谢谢！
