设函数S(x)＝∫0x｜cost｜dt (1)当n为正整数 且nπ≤x＜(n＋1)π时 证明：2n
设函数S(x)＝∫0x｜cost｜dt， (1)当n为正整数，且nπ≤x＜(n＋1)π时，证明：2n≤S(x)＜2(n＋1)； (2)求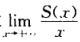
．
请帮忙给出正确答案和分析，谢谢！
参考解答
456***101
2024-11-09 18:54:23
正确答案：(1)nπ≤x＜(n＋1)π时注意到被积函数是非负的于是有 ∫0nπ｜cosx｜dx≤S(x)＜∫0(n＋1)π｜cosx｜dx．又因为｜cosx｜是以π为周期的甬数存每个周期上积分值相等所以 ∫0nπ｜cosx｜dx＝n∫0π｜cosx｜dx＝2n ∫0(n＋1)
[分析求解本题的关键是注意到被积函数｜cost｜是以π为周期的周期函数，从而在每个以π为长度的区间上的积分相等，这样利用积分的可加性可将积分区间分解为以π为长度的区间，进而得到所需的不等式．利用(1)中得到的不等式和夹逼定理即可求(2)中的极限．[评注若f(x)是周期为T的周期函数，即f(xT)＝f(x)，则∫aa＋Tf(x)dx＝∫0Tf(x)dx。
相似问题
设f(x)是区间上的单调 可导函数 且满足 其中f－1是f的反函数 求f(x)．请帮忙给出正确答案和
设f(x)是区间上的单调、可导函数，且满足，其中f－1是f的反函数，求f(x)．请帮忙给出正确答案和分析，谢谢！
设函数f(x)在[0 ＋∞)上可导 f(0)＝0 且其反函数为g(x)．若∫0f(x)g(t)dt＝
设函数f(x)在[0，＋∞)上可导，f(0)＝0，且其反函数为g(x)．若∫0f(x)g(t)dt＝x2ex，求f(x)．请帮忙给出正确答案和分析，谢谢！
试求a的值 使得直线y＝x与曲线y＝logax相切 并求出切点的坐标．请帮忙给出正确答案和分析 谢谢
试求a的值，使得直线y＝x与曲线y＝logax相切，并求出切点的坐标．请帮忙给出正确答案和分析，谢谢！
过坐标原点作曲线y＝lnx的切线 该切线与曲线y＝lnx及x轴围成平面图形D． (1)求D的面积A；
过坐标原点作曲线y＝lnx的切线，该切线与曲线y＝lnx及x轴围成平面图形D． (1)求D的面积A； (2)求D绕直线x＝e旋转一周所得旋转体的体积V．请帮忙给出正
设函数f(x)在区间[a b]上连续 且f(x)＞0 则方程 在开区间(a b)内的根有A．0个．
设函数f(x)在区间[a，b]上连续，且f(x)＞0，则方程 在开区间(a，b)内的根有A．0个．B．1个．C．2个．D．3个．请帮忙给出正确答案和分析，谢谢！
