求下列隐函数的偏导数: 已知平面π经过点P(3 -2 1) 且垂直于P与Q(6 2 7)的连线 求平
求下列隐函数的偏导数: 已知平面π经过点P(3,-2,1),且垂直于P与Q(6,2,7)的连线,求平面π的方程.
已知平面π经过点P(3,-2,1),且垂直于P与Q(6,2,7)的连线,求平面π的方程.
请帮忙给出正确答案和分析,谢谢!
参考解答
正确答案: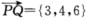 即为所求平面π的法向量又平面过点P(3-21)由点法式方程可得平面π: 3(x-3)+4(y+2)+6(z-1)=0即 3x+4y+6z-7=0
即为所求平面π的法向量又平面过点P(3-21)由点法式方程可得平面π: 3(x-3)+4(y+2)+6(z-1)=0即 3x+4y+6z-7=0
即为所求平面π的法向量,又平面过点P(3,-2,1),由点法式方程可得平面π:3(x-3)+4(y+2)+6(z-1)=0即3x+4y+6z-7=0
相似问题
若函数f(x)存在二阶导数 且其一阶导数的图形如图所示 则曲线y=f(x)的拐点个数为( ). A.
若函数f(x)存在二阶导数,且其一阶导数的图形如图所示,则曲线y=f(x)的拐点个数为( ). A.0B.1C.2D.3请帮忙给出正确答案和分析,谢谢!
若设函数y=y(x)由方程ex+y+cos(xy)=0确定 则设函数y=y(x)由方程ex+y+co
若设函数y=y(x)由方程ex+y+cos(xy)=0确定,则设函数y=y(x)由方程ex+y+cos(xy)=0确定,则请帮忙给出正确答案和分析,谢谢!
设f(x)在(-∞ +∞)内有定义 且则( )。A.x=0必是g(x)的第一类间断点.B.x=0必是
设f(x)在(-∞,+∞)内有定义,且则( )。A.x=0必是g(x)的第一类间断点.B.x=0必是g(x)的第二类间断点.C.x=0必是g(x)的连续点.D.g(x)在点x=0处的连
设函数f(x)在x=a的某个邻域内连续 且f(a)为极大值 则存在δ>0 当x∈(a一δ a+δ)时
设函数f(x)在x=a的某个邻域内连续,且f(a)为极大值,则存在δ>0,当x∈(a一δ,a+δ)时,必有( ).A.(x一a)[f(x)一f(a)]≥0B.(x—a)[f(x)一f(a)]≤0C
设{an} {bn} {cn}均为非负数列 且 则必有( ).A.ann对任意n成立B.bnn对任意
设{an},{bn},{cn}均为非负数列,且,则必有( ).A.ann对任意n成立B.bnn对任意n成立C.极限不存在D.极限不存在请帮忙给出正确答案和分析,谢谢!












