设{an} {bn} {cn}均为非负数列且则必有( )．A．ann对任意n成立B．bnn对任意

大学本科已帮助：人时间:2024-11-16 19:13:00

设{an}，{bn}，{cn}均为非负数列，且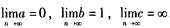
，则必有( )．
A．ann对任意n成立
B．bnn对任意n成立
C．极限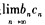不存在
D．极限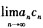不存在
请帮忙给出正确答案和分析，谢谢！

406***102

2024-11-16 19:13:00



正确答案：D
A，B显然不对，因为由数列极限的不等式性质只能得出数列“当n充分大时”的情况，不可能得出“对任意n成立”的性质．C也明显不对，因为“无穷小.无穷大”是未定型，极限可能存在也可能不存在．故应选D．

假设某商品的需求量Q与价格p的函数关系为其中k和r是正的常数证明该商品的需求价格弹性｜E0｜＝r

假设某商品的需求量Q与价格p的函数关系为其中k和r是正的常数，证明该商品的需求价格弹性｜E0｜＝r．请帮忙给出正确答案和分析，谢谢！
若函数y=f(x)有f(x0)= 则当△x→0时该函数在x=x0点外的微分dy是( )．A．与△x

若函数y=f(x)有f(x0)=，则当△x→0时，该函数在x=x0点外的微分dy是( )．A．与△x等价的无穷小B．与△x同阶的无穷小C．经△x低阶的无穷小D．比△x高阶的
设f(x)=xe-2x 求使得f〞(x)＝0的点x．请帮忙给出正确答案和分析谢谢！

设f(x)=xe-2x，求使得f〞(x)＝0的点x．请帮忙给出正确答案和分析，谢谢！
已知某产品的边际成本和边际收益函数分别为Cˊ(q)＝q2－4q+6 Rˊ(q)＝105—2q 固定成

已知某产品的边际成本和边际收益函数分别为Cˊ(q)＝q2－4q+6，Rˊ(q)＝105—2q，固定成本为100，其中q为销售量，C(q)为总成本，R(q)为总收益，求最大利润
求下列函数的偏导数及全微分：把正数a分成3个正数之和使它们的乘积为最大．把正数a分成3个正数之和

求下列函数的偏导数及全微分：把正数a分成3个正数之和，使它们的乘积为最大．把正数a分成3个正数之和，使它们的乘积为最大．请帮忙给出正确答案和分析

假设某商品的需求量Q与价格p的函数关系为其中k和r是正的常数证明该商品的需求价格弹性｜E0｜＝r