如图6—7所示 1mol理想气体循环 cv r为常量 已知a(p0 V0 T0) b(2p0 2V0
如图6—7所示，1mol理想气体循环，cv，r为常量，已知a(p0，V0，T0)，b(2p0，2V0，4T0)，ab为直线过程，bc为绝热过程，ca为等温过程。试求：(1)ab过程热容。(2)循环的效率。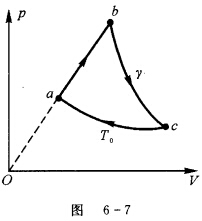 
请帮忙给出正确答案和分析，谢谢！
参考解答
433***994
2024-10-29 12:21:01
正确答案：(1)由题知ab过程方程为p=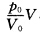
由热容定义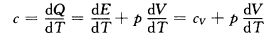
由pV=RT得
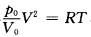微分得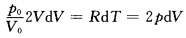
设分子自由度为i有
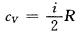代入得热容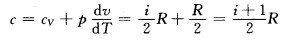
(2)ab过程吸热为
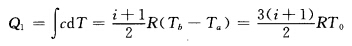bc为绝热过程。 ca为等温过程放热为
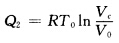又因c为等温过程与绝热过程的交点有 p0V0=pcVc pbVbr=2p0(2V0)=pcVcr
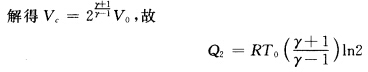循环的效率为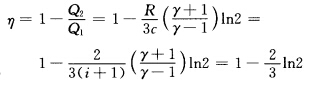
(1)由题知ab过程方程为p=由热容定义由pV=RT,得,微分得设分子自由度为i,有代入得热容(2)ab过程吸热为bc为绝热过程。ca为等温过程,放热为又因c为等温过程与绝热过程的交点,有p0V0=pcVc,pbVbr=2p0(2V0)=pcVcr循环的效率为
相似问题
半径为R的均匀带电球面带电Q 均匀带电直线段长为l 其左端到球心的距离为a 电荷线密度为λ 沿径向放
半径为R的均匀带电球面带电Q，均匀带电直线段长为l，其左端到球心的距离为a，电荷线密度为λ，沿径向放置，如图4—27(a)所示。求均匀带电球面在均匀带电
质点运动学问题是如何分类的?该怎样求解?请帮忙给出正确答案和分析 谢谢！
质点运动学问题是如何分类的?该怎样求解?请帮忙给出正确答案和分析，谢谢！
一个质点作如图1—3所示的斜抛运动 忽略空气阻力。试问： (3)法向加速度an是否变化? (4)
一个质点作如图1—3所示的斜抛运动，忽略空气阻力。试问： (3)法向加速度an是否变化? (4)图1-3所示轨道曲率半径何处最大?何处最小?其数值是多少?请
p一V图上循环曲线如图6—5所示 其中ab为绝热线 bc为等体线 ca为等温线。已知v2=2v1 等
p一V图上循环曲线如图6—5所示，其中ab为绝热线，bc为等体线，ca为等温线。已知v2=2v1，等温过程温度为T1，工质为1 mol，双原子理想气体分子。求此循环1
半径为R1均匀带电球体 带电体密度为ρ 在其中挖去半径为r1的小球体 球心距为OO’=d 如图4—1
半径为R1均匀带电球体，带电体密度为ρ，在其中挖去半径为r1的小球体，球心距为OO’=d，如图4—17所示。求小球内的电势分布。 请帮忙给出正确答案和分析，谢谢！
