质点运动学问题是如何分类的?该怎样求解?请帮忙给出正确答案和分析 谢谢！

正确答案：质点运动学问题按照求解时所用数学的不同大致可分为如下两类： 第一类：已知运动学方程或变相已知运动学方程(如已知轨迹方程)而求速度和加速度。 第二类：已知速度求运动学方程或已知加速度求速度和运动学方程几何参量等。 求解方法如下： 第一类问题只需按定义式将已知的运动运动学方程代入即可得解。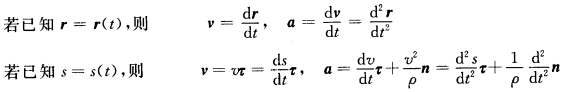对已知的运动学方程求导即得。 若已知轨迹方程则对轨迹方程两边求导再由题给条件就可求解。更细的分类就不在此一一列举了。 第二类问题常用积分法(微分的逆运算)或解微分方程。例如：已知加速度求速度和运动方程。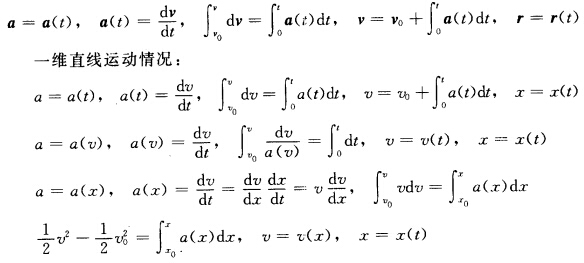圆周运动有θ=θ(t)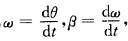v＝ωRa_τ=ωRa_τ=Rβa_n=ω²R其解法与上面大致相同用自然坐标系或曲线坐标系来处理问题其方法技巧类似。初学者常见错误为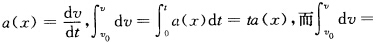=∫₀^ta(v)dt=ta(v)变为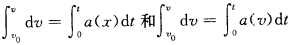不能算错变换为求解积分方程但由于数学知识所限初学者通常解不出来。
质点运动学问题按照求解时所用数学的不同,大致可分为如下两类：第一类：已知运动学方程或变相已知运动学方程(如已知轨迹方程),而求速度和加速度。第二类：已知速度求运动学方程,或已知加速度求速度和运动学方程,几何参量等。求解方法如下：第一类问题只需按定义式,将已知的运动运动学方程代入即可得解。对已知的运动学方程求导即得。若已知轨迹方程,则对轨迹方程两边求导,再由题给条件就可求解。更细的分类,就不在此一一列举了。第二类问题常用积分法(微分的逆运算)或解微分方程。例如：已知加速度,求速度和运动方程。圆周运动有θ=θ(t),v＝ωR,aτ=ωR,aτ=Rβ,an=ω2R,其解法与上面大致相同,用自然坐标系或曲线坐标系来处理问题,其方法技巧类似。初学者常见错误为=∫0ta(v)dt=ta(v)变为不能算错,变换为求解积分方程,但由于数学知识所限,初学者通常解不出来。