证明：(2 i 1－i)与(2＋2i 1－i 2i)表示一对共轭复点 并求其连线方程．请帮忙给出正确
证明：(2，i，1－i)与(2＋2i，1－i，2i)表示一对共轭复点，并求其连线方程．
请帮忙给出正确答案和分析，谢谢！
参考解答
432***102
2024-11-19 22:48:39
正确答案：点(2i1－i)之非齐次坐标为(1＋i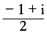
)点(2＋2i1－i2i)之非齐次坐标为(1－i
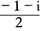) 显然其坐标为共轭复数所以此二点为共轭复点．其连线方程
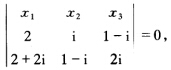即χ1－2χ2－2χ3＝0．
点(2,i,1－i)之非齐次坐标为(1＋i,),点(2＋2i,1－i,2i)之非齐次坐标为(1－i,)显然其坐标为共轭复数,所以此二点为共轭复点．其连线方程即χ1－2χ2－2χ3＝0．
相似问题
设A B C D E为五个共线点 求证：(AB CD).(AB DE).(AB EC)＝1．请帮忙给
设A、B、C、D、E为五个共线点，求证：(AB，CD) (AB，DE) (AB，EC)＝1．请帮忙给出正确答案和分析，谢谢！
求作下列图形的对偶图形． 设A1A2A3是坐标三点形O(1 1 1)为一定点 A1O A2O A3O
求作下列图形的对偶图形． 设A1A2A3是坐标三点形O(1，1，1)为一定点，A1O，A2O，A3O分别与A2A3、A3A1、A设A1A2A3是坐标三点形O(1，1，1)为一定点，A1O，
求：(1)过点(1 －i 2)的实直线； (2)直线[i 2 1－i]上的实点； (3)求证：(1＋
求：(1)过点(1，－i，2)的实直线； (2)直线[i，2，1－i]上的实点； (3)求证：(1＋i，－1＋i)，(1，1＋i)，(i，－1－i)三点共线，并求其上之实点．请帮
求证：三点(1 －i 0) (1 i 0) (1 －1 0)共线 将最后一点的坐标表示为前两点的线性
求证：三点(1，－i，0)，(1，i，0)，(1，－1，0)共线，将最后一点的坐标表示为前两点的线性组合．请帮忙给出正确答案和分析，谢谢！
求射影变换式 使它的不变元素的参数是λ1＝－1 λ2＝3 并且使λ3＝1变成λ′3＝0．请帮忙给出正
求射影变换式，使它的不变元素的参数是λ1＝－1，λ2＝3，并且使λ3＝1变成λ′3＝0．请帮忙给出正确答案和分析，谢谢！
