求作下列图形的对偶图形. 如图1—2—21 设以三直线α=O β=0 γ=0为边的三线形 l1 l2
求作下列图形的对偶图形. 如图1—2—21,设以三直线α=O,β=0,γ=0为边的三线形,l1、l2、l3,分别为通过
如图1—2—21,设以三直线α=O,β=0,γ=0为边的三线形,l1、l2、l3,分别为通过三个顶点的三直线,求证:l1,l2,l3共点的充要条件是其方程可以表示为pβ-rγ)=0,rγ-pα=0,pα-qβ=0(其中p,q,r为常数).写出其对偶命题. 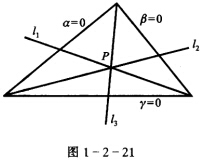
请帮忙给出正确答案和分析,谢谢!
参考解答
正确答案:充分性显然只证明必要性.如图2—2—17.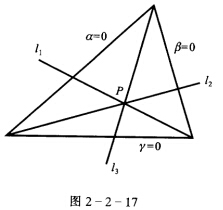 l1l2l3的方程可以分别表示为: mβ+n′γ=0 nγ+l′α=0. lα+m′β=0. 如果三直线共点则有实数λ1、λ2、λ3(λ1λ2λ3≠0)存在使λ1(mβ+n′γ)+λ2(nγ+l′α)+λ3(lα+m′β)=0. 令λ1m=qλ1n′=r′λ2n=rλ2l′=p′λ3l=pλ3m′=q′. 则得(P+P′)α+(q+q′)β+(r+r′)y=0. 因为α=0β=0γ=0不共点所以 P+P′=q+q′=r+r′=0. ① 由于λ1λ2λ3≠0所以
l1l2l3的方程可以分别表示为: mβ+n′γ=0 nγ+l′α=0. lα+m′β=0. 如果三直线共点则有实数λ1、λ2、λ3(λ1λ2λ3≠0)存在使λ1(mβ+n′γ)+λ2(nγ+l′α)+λ3(lα+m′β)=0. 令λ1m=qλ1n′=r′λ2n=rλ2l′=p′λ3l=pλ3m′=q′. 则得(P+P′)α+(q+q′)β+(r+r′)y=0. 因为α=0β=0γ=0不共点所以 P+P′=q+q′=r+r′=0. ① 由于λ1λ2λ3≠0所以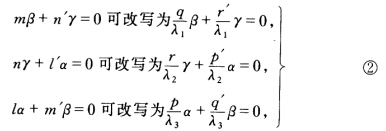 由①、②得l1、l2、l3的方程可以分别表示为: qβrγ=0 rγ-pα=0 pα-qβ=0.
由①、②得l1、l2、l3的方程可以分别表示为: qβrγ=0 rγ-pα=0 pα-qβ=0.
充分性显然,只证明必要性.如图2—2—17.l1,l2,l3的方程可以分别表示为:mβ+n′γ=0,nγ+l′α=0.lα+m′β=0.如果三直线共点,则有实数λ1、λ2、λ3(λ1λ2λ3≠0)存在,使λ1(mβ+n′γ)+λ2(nγ+l′α)+λ3(lα+m′β)=0.令λ1m=q,λ1n′=r′,λ2n=r,λ2l′=p′,λ3l=p,λ3m′=q′.则得(P+P′)α+(q+q′)β+(r+r′)y=0.因为α=0,β=0,γ=0不共点,所以P+P′=q+q′=r+r′=0.①由于λ1λ2λ3≠0,所以由①、②得l1、l2、l3的方程可以分别表示为:qβrγ=0,rγ-pα=0,pα-qβ=0.
相似问题
证明:(2 i 1-i)与(2+2i 1-i 2i)表示一对共轭复点 并求其连线方程.请帮忙给出正确
证明:(2,i,1-i)与(2+2i,1-i,2i)表示一对共轭复点,并求其连线方程.请帮忙给出正确答案和分析,谢谢!
设A B C D E为五个共线点 求证:(AB CD).(AB DE).(AB EC)=1.请帮忙给
设A、B、C、D、E为五个共线点,求证:(AB,CD) (AB,DE) (AB,EC)=1.请帮忙给出正确答案和分析,谢谢!
求作下列图形的对偶图形. 设A1A2A3是坐标三点形O(1 1 1)为一定点 A1O A2O A3O
求作下列图形的对偶图形. 设A1A2A3是坐标三点形O(1,1,1)为一定点,A1O,A2O,A3O分别与A2A3、A3A1、A设A1A2A3是坐标三点形O(1,1,1)为一定点,A1O,
求:(1)过点(1 -i 2)的实直线; (2)直线[i 2 1-i]上的实点; (3)求证:(1+
求:(1)过点(1,-i,2)的实直线; (2)直线[i,2,1-i]上的实点; (3)求证:(1+i,-1+i),(1,1+i),(i,-1-i)三点共线,并求其上之实点.请帮
求证:三点(1 -i 0) (1 i 0) (1 -1 0)共线 将最后一点的坐标表示为前两点的线性
求证:三点(1,-i,0),(1,i,0),(1,-1,0)共线,将最后一点的坐标表示为前两点的线性组合.请帮忙给出正确答案和分析,谢谢!












