设A B为n阶方阵 且对 有｜λE—A｜=｜λE一B｜ 则( )．A．｜λE+A｜=｜λE+B｜B．
设A、B为n阶方阵，且对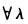
，有｜λE—A｜=｜λE一B｜，则( )．
A．｜λE+A｜=｜λE+B｜
B．A与B相似
C．A与B合同
D．A、B同时可对角化或A、B同时不可对角化
请帮忙给出正确答案和分析，谢谢！
参考解答
432***102
2024-11-16 01:26:12
正确答案：A
由｜λE—A｜=｜λE一B｜知，A、B具有相同的特征值λ1，λ2，…λn，即｜λE—A｜=｜λE一B｜=(λ—λ1)(λ—λ2)…(λ—λ2)，而一A，一B的特征值为一λ1，一λ2，…，一λn，所以｜λE一(一A)｜=｜λE一(一B)｜=(λ1+λ1)…(λ+λn)，即｜λE+A｜=｜λE+B｜．B,C,D均可举反例说明不成立．其中C项不正确是显然的，因为A、B合同，其前提是A、曰为对称矩阵．反例：如A则A、B的特征多项式相同，但A、B不相似，否则P-1AP=B→A=PBP-1=PEP-1=E，矛盾，可排除B,D.
相似问题
已知n阶方阵(一∞ 0)U(0 ＋∞) 当a≠b且a≠一(n一1)b时 秩A=_____n阶方阵(一
已知n阶方阵(一∞，0)U(0，＋∞)，当a≠b且a≠一(n一1)b时，秩A=_____n阶方阵(一∞，0)U(0，+∞)，当a≠b且a≠一(n一1)b时，秩A=_____请帮忙给出正确答案和分析，谢谢！
设设A B均为三阶矩阵 E是三阶单位矩阵．已知AB＝2A＋B B＝ 则(A—E)－1＝_______
设设A，B均为三阶矩阵，E是三阶单位矩阵．已知AB＝2A＋B，B＝，则(A—E)－1＝_______．设A，B均为三阶矩阵，E是三阶单位矩阵．已知AB＝2A＋B，B＝，则(A
设A=1/2(B+E) 则当且仅当B2=________时 A2=A．请帮忙给出正确答案和分析 谢谢
设A=1 2(B+E)，则当且仅当B2=________时，A2=A．请帮忙给出正确答案和分析，谢谢！
α=(1 2 3 4) β=[1 1/2 1/3 1/4] A=αTβ 求An(n为正整数)．请帮忙
α=(1，2，3，4)，β=[1，1 2，1 3，1 4]，A=αTβ，求An(n为正整数)．请帮忙给出正确答案和分析，谢谢！
设向量组α1 α2 α3线性无关 向量β1可由α1 α2 α3线性表示 而向量β2不能由α1 α2
设向量组α1，α2，α3线性无关，向量β1可由α1，α2，α3线性表示，而向量β2不能由α1，α2，α3线性表示，则对于任意常数k，必有A．α1，α2，α3，k
