我国某海区有相隔甚远的两块大型渔场 每只渔船每次出海能捕捞鱼的数量与渔船数有关。渔场1鱼群丰富 每只

正确答案：当对出海捕鱼没有限制时每条渔船都各自追求自己的利润最大化。在渔场1每条渔船的利润为 π₁＝Pq₁－TC₁=50－0．02N₁－10 只要利润还大于零就会有新的渔船进入直到每条渔船的利润为零。 N₁＝2000条每条船每次捕10吨鱼利润为零。 在渔场2每条渔船的利润为 π₂＝Pq₂－TC₂＝25－0．1N₂－10 N₂＝250条每条船每次也捕10吨鱼利润也为零。 如果限制出海渔船为1610条那么哪个渔场利润大渔船就去哪里直到两个渔场的利润相等。 50－0．02N₁－10＝25－0．1N₂－10 N₁＋N₂＝1610 N₁＝1550条N₂＝60条每条渔船捕鱼19吨利润为9万元总利润为14490万元。 如果为了捕鱼总利润最大化： π＝π₁＋π₂＝PN₁q₁－N₁TC₁＋PN₂q₂－N₂TC₂ ＝50N₁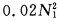－－10N₁＋25N₂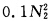－－10N₂ N₁＝1000条N₂＝75条在渔场1每条渔船能捕30吨在渔场2每条渔船能捕17．5吨共获利润20562．5万元。
当对出海捕鱼没有限制时,每条渔船都各自追求自己的利润最大化。在渔场1,每条渔船的利润为π1＝Pq1－TC1=50－0．02N1－10只要利润还大于零,就会有新的渔船进入,直到每条渔船的利润为零。N1＝2000条,每条船每次捕10吨鱼,利润为零。在渔场2,每条渔船的利润为π2＝Pq2－TC2＝25－0．1N2－10N2＝250条,每条船每次也捕10吨鱼,利润也为零。如果限制出海渔船为1610条,那么,哪个渔场利润大,渔船就去哪里,直到两个渔场的利润相等。50－0．02N1－10＝25－0．1N2－10N1＋N2＝1610N1＝1550条,N2＝60条,每条渔船捕鱼19吨,利润为9万元,总利润为14490万元。如果为了捕鱼总利润最大化：π＝π1＋π2＝PN1q1－N1TC1＋PN2q2－N2TC2＝50N1－－10N1＋25N2－－10N2N1＝1000条,N2＝75条,在渔场1每条渔船能捕30吨,在渔场2每条渔船能捕17．5吨,共获利润20562．5万元。