飞机降落时的着陆速度大小v =90 km.h-1 方向与地面平行 飞机与地面间的摩擦系数μ?=0.1
飞机降落时的着陆速度大小v =90 km.h-1，方向与地面平行，飞机与地面间的摩擦系数μ?=0.10，迎面空气阻力为Cxv2，升力为Cyv2（v是飞机在跑道上的滑行速度, Cx和Cy均为常量）。已知飞机的升阻比K=Cy /Cx=5。求飞机从着地到停止这段时间所滑行的距离。设飞机刚着地时对地面无压力。
请帮忙给出正确答案和分析，谢谢！
参考解答
420***100
2024-11-04 10:54:42
正确答案：以飞机为研究对象则飞机着陆后受力如图2-5所示。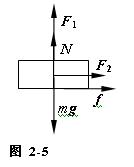
图中F1=Cyv2F2=Cxv2。由题设知飞机刚着陆时对地面无压力则N0=0速度为v0。由牛顿运动定律有0=F1-mg即
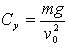（1）又因飞机的升阻比K=Cy /Cx=5可得
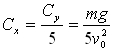（2）建立平面直角坐标系则由牛顿运动定律可得到沿坐标轴方向的动力学方程分别为0=N+F1-mg （3）
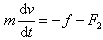（4）根据摩擦力定义可得F=μN （5）将式（1）、（2）、（3）、（4）和（5）联立求解有
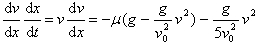（6）整理式（6）并做积分有
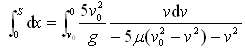（7）完成积分并求解上式可得到飞机需滑行的距离为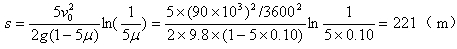
以飞机为研究对象,则飞机着陆后受力如图2-5所示。图中F1=Cyv2,F2=Cxv2。由题设知,飞机刚着陆时对地面无压力,则N0=0,速度为v0。由牛顿运动定律有0=F1-mg,即（1）又因飞机的升阻比K=Cy/Cx=5,可得（2）建立平面直角坐标系,则由牛顿运动定律可得到沿坐标轴方向的动力学方程分别为0=N+F1-mg（3）（4）根据摩擦力定义可得F=μN（5）将式（1）、（2）、（3）、（4）和（5）联立求解有（6）整理式（6）并做积分有（7）完成积分,并求解上式可得到飞机需滑行的距离为
相似问题
一个质点作直线运动 某时刻的瞬时速度v=2m·s-1 瞬时加速度a=2m·s-2 则一秒钟后质点的速
一个质点作直线运动，某时刻的瞬时速度v=2m·s-1，瞬时加速度a=2m·s-2，则一秒钟后质点的速度( )．A．等于零B．大于2m·s-1C．等于2m·s-1D．不能确定
流体流动过程中 稳定性指的是_________ 定态性指的是__________。请帮忙给出正确答案
流体流动过程中，稳定性指的是_________，定态性指的是__________。请帮忙给出正确答案和分析，谢谢！
一条质量为M且分布均匀的绳子 其长度为ι0 一端拴在转轴上 并以恒定角速度ω在水平面上旋转．设在转动
一条质量为M且分布均匀的绳子，其长度为ι0，一端拴在转轴上，并以恒定角速度ω在水平面上旋转．设在转动过程中绳子始终伸直，且忽略重力与空气阻力，求
现需用两台相同的离心泵将河水送人一密闭的高位槽．高位槽液面上方压强为1．5 atm(表压强) 高位槽
现需用两台相同的离心泵将河水送人一密闭的高位槽．高位槽液面上方压强为1．5 atm(表压强)，高位槽液面与河水水面之间的垂直高度为1 0 m，已知整个管
量纲分析法的目的在于( )。A．得到各变量间的确切定量关系B．用无量纲数群代替变量 使实验与关联简化
量纲分析法的目的在于( )。A．得到各变量间的确切定量关系B．用无量纲数群代替变量，使实验与关联简化C．得到无量纲数群问定量关系D．无需进行实验，即
