一条质量为M且分布均匀的绳子 其长度为ι0 一端拴在转轴上 并以恒定角速度ω在水平面上旋转．设在转动
一条质量为M且分布均匀的绳子，其长度为ι0，一端拴在转轴上，并以恒定角速度ω在水平面上旋转．设在转动过程中绳子始终伸直，且忽略重力与空气阻力，求距转轴为r处绳中的张力．
请帮忙给出正确答案和分析，谢谢！
参考解答
413***100
2024-11-04 10:28:33
正确答案：绳子在水平面内转动时由于绳上各段转动速度不同所以各处绳子的张力也不同．任意选取距轴为r处的一段绳元长度为dr．质量为dm=(M/ι0)dr．设左、右两侧的绳子对它的拉力分别为T(r)和T(r+dr)如图2—5所示．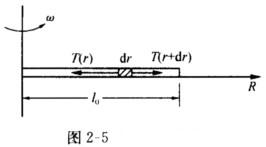
这段绳元做圆周运动根据牛顿第二定律列出法向方程得到
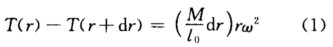经整理得到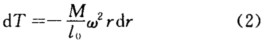
因绳子的末端是自由端即r=ι0时T=0．对式(2)的两端积分有
最后得到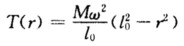
①隔离体法不仅可用在由几个物体组成的离散物体系统上，也可以用在质量连续分布的物体系统(如固液、液体等)上．本题就是将绳子看成由一系列微小绳段组成的连续物体系统的．这种方法是微积分思想的体现，常用来分析求解这类系统内某处的内力、应力或形变等问题．②由计算结果可知，绳子内的张力不是均匀的，越靠近转轴处，绳子内的张力越大．而末端是自由端，故张力T=0．
相似问题
现需用两台相同的离心泵将河水送人一密闭的高位槽．高位槽液面上方压强为1．5 atm(表压强) 高位槽
现需用两台相同的离心泵将河水送人一密闭的高位槽．高位槽液面上方压强为1．5 atm(表压强)，高位槽液面与河水水面之间的垂直高度为1 0 m，已知整个管
量纲分析法的目的在于( )。A．得到各变量间的确切定量关系B．用无量纲数群代替变量 使实验与关联简化
量纲分析法的目的在于( )。A．得到各变量间的确切定量关系B．用无量纲数群代替变量，使实验与关联简化C．得到无量纲数群问定量关系D．无需进行实验，即
如图1—29所示的管路 用离心泵将池A中水输送至高位槽中 已知离心泵的特性曲线为He=25-0．00
如图1—29所示的管路，用离心泵将池A中水输送至高位槽中，已知离心泵的特性曲线为He=25-0．004qv2(He的单位为m；qv的单位为m3／h)。吸入管路的阻力损失为
一颗质量为m的珠子系在线的一端 线的另一端固定在天花板上 线长为l0先拉动珠子使线保持水平静止 然后
一颗质量为m的珠子系在线的一端，线的另一端固定在天花板上，线长为l0先拉动珠子使线保持水平静止，然后松手使珠子下落。求摆下角度q时这个珠子的速率和
已知某质点的运动学方程为x=5+2t—2t2 单位为SI制．求： (1)质点在第2s内通过的位移；
已知某质点的运动学方程为x=5+2t—2t2，单位为SI制．求： (1)质点在第2s内通过的位移； (2)该质点在第0．3s和第1s末的速度和加速度； (3)问质点做什么
