求χ2＋y2＝r2的动切线关于aχ2＋by2＝1的极点的轨迹方程．请帮忙给出正确答案和分析 谢谢！

正确答案：将已知曲线方程化为齐次式： χ²＋y²＝r²化为χ₁²＋χ₂²－r²χ₃²＝0 ① aχ²＋by²＝1化为aχ₁²＋bχ₂²－χ₃²＝0． ② 在①上任取一点(χ′₁χ′₂χ′₃)则切线方程为： χ′χ₁＋χ′χ₂－r²χ′χ₃＝0． ③ 设直线③关于aχ₁²＋bχ₂²－χ₃²＝0的极点为[χ₁χ₂χ₃则有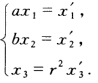： 又因为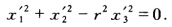． 所以(aχ₁)²＋(bχ₂)²－r2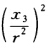＝0 即r²(a²χ₁²＋b²χ₂²)－χ₃²＝0． 此即所求极点的轨迹方程其非齐次坐标方程为： r²(a²χ²＋b²y²)＝1．
将已知曲线方程化为齐次式：χ2＋y2＝r2化为χ12＋χ22－r2χ32＝0,①aχ2＋by2＝1化为aχ12＋bχ22－χ32＝0．②在①上任取一点(χ′1,χ′2,χ′3),则切线方程为：χ′χ1＋χ′χ2－r2χ′χ3＝0．③设直线③关于aχ12＋bχ22－χ32＝0的极点为[χ1,χ2,χ3,则有：又因为．所以(aχ1)2＋(bχ2)2－r2＝0,即r2(a2χ12＋b2χ22)－χ32＝0．此即所求极点的轨迹方程,其非齐次坐标方程为：r2(a2χ2＋b2y2)＝1．