有一列平面简谐波 其波动方程为 求：(1)在什么时刻 在坐标原点x=0处会第一次出现波峰?(2)当t
有一列平面简谐波，其波动方程为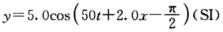
，求：(1)在什么时刻，在坐标原点x=0处会第一次出现波峰?(2)当t2=1．0s时，最靠近坐标原点的波峰位置距原点多远?
请帮忙给出正确答案和分析，谢谢！
参考解答
413***100
2024-11-04 00:01:02
正确答案：×
(1)所谓出现波峰,即位移等于正最大,将x=0和y=5．0m代入波动方程中,有解得50t—π/2=±2kπ(2)题意要求第一次出现波峰,故取k=0．由此得出原点处第一次出现波峰的时刻为t1=π/100=0．0314(s)(2)从波动方程可知,ω=50rad．s-1,2π/λ=2．0m-1．于是,波长和周期分别为λ=2π/2．0=3．14(m)T=2π/ω=2π/50=0．1257(s)从原点处第一次出现波峰的时间t1=0．0314s到t2=1．0s,经过的时间是△t=t2—t2=0．9686s经过的周期为△N=△t/T=7．71从波动方程得知,波向OX轴负向传播．经过7．71个周期,波峰向OX轴负向移动了7．71λ．因此,t2=1．0s时,靠近原点最近的两个波峰,其位置离原点的距离分别为左边：x=7．71λ—7λ=0．71×3．14=2．23(m)右边：x'=λ—x=3．14—2．23=0．91(m)
相似问题
一个弹簧振子和一个单摆(只考虑小幅度摆动) 在地面上的固有振动周期分别为T1和T2将它们拿到月球上去
一个弹簧振子和一个单摆(只考虑小幅度摆动)，在地面上的固有振动周期分别为T1和T2将它们拿到月球上去，相应的周期分别为T1和T2，则有( )．A．T1"＞T1且T
如图7-13所示 S1和S2为同相位的两相干波源 相距为L 点P距S1为r；波源S1在点P引起的振动
如图7-13所示，S1和S2为同相位的两相干波源，相距为L，点P距S1为r；波源S1在点P引起的振动振幅为A1，波源S2在点P引起的振动振幅为A2，两波波长都是λ，则
如图4-1所示 力F通过一条不可伸长的绳子和一根劲度为200N.m-1的轻弹簧 绕过滑轮缓慢地拉地面
如图4-1所示，力F通过一条不可伸长的绳子和一根劲度为200N m-1的轻弹簧、绕过滑轮缓慢地拉地面上质量为2 0kg的物体，忽略滑轮质量及摩擦。求自刚将绳子拉
一列平面简谐波以速度u沿X轴正向传播 在t=t时波形曲线如图7-6所示 则坐标原点O的振动方程为(
一列平面简谐波以速度u沿X轴正向传播，在t=t时波形曲线如图7-6所示，则坐标原点O的振动方程为( )． A． B． C． D． 请帮忙给出正确答案和分析，谢谢！
如图4-9所示 一个斜面倾角为θ 用与斜面成a角的恒力F将一个质量为m的物体沿斜面拉升了高度h 物体
如图4-9所示，一个斜面倾角为θ，用与斜面成a角的恒力F将一个质量为m的物体沿斜面拉升了高度h，物体与斜面间的摩擦系数为μ．摩擦力在此过程中所做的功为
