劲度为k的轻弹簧 上端连接一块质量为m的平板A 处于平衡状态。如图6-4所示。另有一个质量为m的物体
劲度为k的轻弹簧,上端连接一块质量为m的平板A,处于平衡状态。如图6-4所示。另有一个质量为m的物体自平板A上方h处自由下落,与平板发生完全非弹性碰撞。平板开始向下运动时开始计时。试求系统的运动学方程(设竖直向上为Y轴正向) 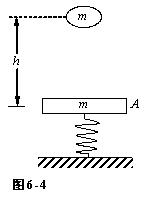
请帮忙给出正确答案和分析,谢谢!
参考解答
正确答案:设系统的运动学方程为y=Acos(ωt+ψ)要求系统的运动学方程关键是要确定A、ω和ψ。ω的确定:设碰撞前系统的平衡位置在O’处碰撞后系统的平衡位置在O处且碰撞之后系统的总质量为2m 利用平衡条件有k|OO’|=2mg那么任一时刻系统在点y处受合外力作用所满足的等式为-k(y-OO’)-2mg=2ma (1)解式(1)可得 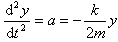 于是可得到系统振动的角频率为
于是可得到系统振动的角频率为 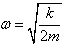 (2)A的确定:设碰撞之前平板A的平衡位置在O’’处该处平衡条件为KOO’’=mg物体与平板在该处发生碰撞且认为在碰撞瞬间位置不变因此碰撞后系统运动的起始位置y0=OO’’=
(2)A的确定:设碰撞之前平板A的平衡位置在O’’处该处平衡条件为KOO’’=mg物体与平板在该处发生碰撞且认为在碰撞瞬间位置不变因此碰撞后系统运动的起始位置y0=OO’’=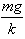 (3)碰撞瞬间系统所受合外力为零故系统动量守恒可得mv=2mv0 (4)其中由机械能守恒可得到碰撞之前物体的速度为
(3)碰撞瞬间系统所受合外力为零故系统动量守恒可得mv=2mv0 (4)其中由机械能守恒可得到碰撞之前物体的速度为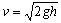 (5)解式(4)后将式(5)代入可得碰撞后物体的速度为
(5)解式(4)后将式(5)代入可得碰撞后物体的速度为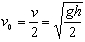 (6)由初始条件式(3)和式(6)可得到系统振动的振幅为
(6)由初始条件式(3)和式(6)可得到系统振动的振幅为 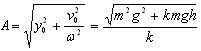 (7) 初相ψ的确定:t=0时系统在O’’点由式(3)可得
(7) 初相ψ的确定:t=0时系统在O’’点由式(3)可得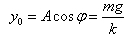 解上式可得
解上式可得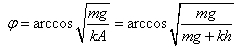 (9)将式(2)、(7)和(9)代入运动方程可得系统的运动方程为
(9)将式(2)、(7)和(9)代入运动方程可得系统的运动方程为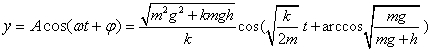
设系统的运动学方程为y=Acos(ωt+ψ),要求系统的运动学方程,关键是要确定A、ω和ψ。ω的确定:设碰撞前系统的平衡位置在O’处,碰撞后系统的平衡位置在O处,且碰撞之后系统的总质量为2m,利用平衡条件有k|OO’|=2mg那么任一时刻系统在点y处受合外力作用所满足的等式为-k(y-OO’)-2mg=2ma(1)解式(1)可得于是可得到系统振动的角频率为(2)A的确定:设碰撞之前平板A的平衡位置在O’’处,该处平衡条件为KOO’’=mg,物体与平板在该处发生碰撞,且认为在碰撞瞬间位置不变,因此,碰撞后系统运动的起始位置y0=OO’’=(3)碰撞瞬间系统所受合外力为零,故系统动量守恒,可得mv=2mv0(4)其中,由机械能守恒可得到碰撞之前物体的速度为(5)解式(4)后将式(5)代入,可得碰撞后物体的速度为(6)由初始条件式(3)和式(6),可得到系统振动的振幅为(7)初相ψ的确定:t=0时,系统在O’’点,由式(3)可得解上式可得(9)将式(2)、(7)和(9)代入运动方程,可得系统的运动方程为
相似问题
一束光是自然光和线偏振光的混合光 让它垂直通过一个偏振片.若以此入射光束为轴旋转偏振片 测得透射光强
一束光是自然光和线偏振光的混合光,让它垂直通过一个偏振片.若以此入射光束为轴旋转偏振片,测得透射光强度最大值是最小值的5倍,那么入射光束中自然光
一束光强为I0的自然光 相继通过三个偏振片P1 P2 P3后 出射光的光强为I= I0/8。已知P1
一束光强为I0的自然光,相继通过三个偏振片P1、P2、P3后,出射光的光强为I= I0 8。已知P1和P3的偏振化方向互相垂直。若以入射光为轴,旋转P2,问P2最少
氦氖激光器发出波长为632.8nm的单色光 射在相距2.2×10-4m的双缝上.在距离双缝1.80m
氦氖激光器发出波长为632.8nm的单色光,射在相距2.2×10-4m的双缝上.在距离双缝1.80m处的屏幕上呈现干涉图样.求20条明条纹之间的距离.请帮忙给出正
用平行的白光垂直入射在平面透射光栅上时 波长为λ1=440nm的第3级光谱线将与波长为λ2=____
用平行的白光垂直入射在平面透射光栅上时,波长为λ1=440nm的第3级光谱线将与波长为λ2=__________nm的第2级光谱线重叠.请帮忙给出正确答案和分析,谢谢!
用平行光管把某光源发出的单色光变成平行光后照射在宽度a=0.308mm的单缝上 用焦距为f=12.6
用平行光管把某光源发出的单色光变成平行光后照射在宽度a=0.308mm的单缝上,用焦距为f=12.62cm的测微目镜测得中央明条纹两侧的第5级暗条纹之间的距离为












