设曲线y＝ax2(a＞0 x≥0)与y＝1－x2交于点A 过坐标原点O和点A的直线与曲线y＝ax2围
设曲线y＝ax2(a＞0，x≥0)与y＝1－x2交于点A，过坐标原点O和点A的直线与曲线y＝ax2围成一平面图形，问a为何值时，该图形绕x轴旋转一周所得的旋转体体积最大?最大体积是多少?
请帮忙给出正确答案和分析，谢谢！
参考解答
413***101
2024-11-09 16:37:06
正确答案：当x≥0时由
故直线OA的方程为
于是旋转体的体积为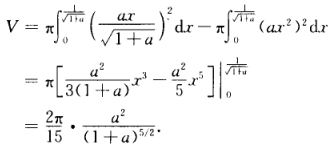
从而有
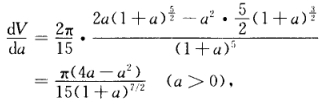令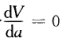
并由a＞0得唯一驻点a＝4．由题意知此旋转体体积在a＝4时取最大值其最大体积为
本题是高等数学在几何上的综合应用问题(如图1—3—6)．应先求出交点A的坐标，再导出旋转体的体积，它是参数a的函数，求此函数的最值即可．
相似问题
已知函数y＝f(x)对一切x满足xf〞(x)＋x2fˊ(x)＝ex－1 若fˊ(x。)＝0(x。≠0
已知函数y＝f(x)对一切x满足xf〞(x)＋x2fˊ(x)＝ex－1，若fˊ(x。)＝0(x。≠0)，则( )．A．f(x。)是f(x)的极大值B．f(x。)是f(x)的极小值C．f(x。)不是f
下列广义积分中收敛的是A．B．C．D．请帮忙给出正确答案和分析 谢谢！
下列广义积分中收敛的是A．B．C．D．请帮忙给出正确答案和分析，谢谢！
设f(x)是连续函数 且 则F(x)等于A．B．C．D．请帮忙给出正确答案和分析 谢谢！
设f(x)是连续函数，且，则F(x)等于A．B．C．D．请帮忙给出正确答案和分析，谢谢！
设f(x)在[0 1]上连续 在(0 1)内可导 且满足 证明：存在一点ξ∈(0 1) 使得f(ξ)
设f(x)在[0，1]上连续，在(0，1)内可导，且满足，证明：存在一点ξ∈(0，1)，使得f(ξ)＝2ξf(ξ)．请帮忙给出正确答案和分析，谢谢！
设m n是正整数 则反常积分的收敛性A．仅与m值有关．B．仅与n值有关．C．与m n值都有关．D．与
设m，n是正整数，则反常积分的收敛性A．仅与m值有关．B．仅与n值有关．C．与m，n值都有关．D．与m，n值都无关．请帮忙给出正确答案和分析，谢谢！
