找出如下博弈中A B两人的Nash—Equilibrium(含混合策略的均衡)(北京大学国家发展研究
找出如下博弈中A、B两人的Nash—Equilibrium(含混合策略的均衡)(北京大学国家发展研究院2006研) 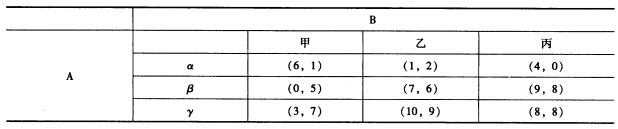
请帮忙给出正确答案和分析,谢谢!
参考解答
正确答案:使用严格剔除劣策略法来求解。 对于B来讲乙严格占优于甲因此B肯定不会选择甲于是剔除甲策略。在剩余的矩阵中对于A来讲β严格占优于α所以A不会选择α于是再剔除α策略。 重复严格剔除劣策略后矩阵变为: (1)分析如下:A选β时B最优的选择是丙因为8>6;A选γ时B最优的选择是乙因为9>8;B选乙时A最优的选择是γ因为10>7;B选丙时A最优的选择是β因为9>7。可得出(γ乙)(β丙)是纯策略均衡。(2)另外该博弈还有一个混合策略均衡求解如下:设A以p的概率选择策略βB以q的概率选择策略乙则根据同等支付原则有: 7q+9(1一q)=10q+8(1一q) 6p+9(1一p)=8p+8(1一p)
(1)分析如下:A选β时B最优的选择是丙因为8>6;A选γ时B最优的选择是乙因为9>8;B选乙时A最优的选择是γ因为10>7;B选丙时A最优的选择是β因为9>7。可得出(γ乙)(β丙)是纯策略均衡。(2)另外该博弈还有一个混合策略均衡求解如下:设A以p的概率选择策略βB以q的概率选择策略乙则根据同等支付原则有: 7q+9(1一q)=10q+8(1一q) 6p+9(1一p)=8p+8(1一p)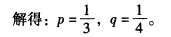 因此
因此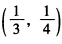 是一个混合策略均衡表示A以
是一个混合策略均衡表示A以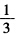 的概率选择β
的概率选择β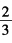 的概率选择γ;B以
的概率选择γ;B以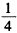 的概率选择乙
的概率选择乙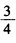 的概率选择丙时这个混合策略组合就构成了一个纳什均衡。
的概率选择丙时这个混合策略组合就构成了一个纳什均衡。
使用严格剔除劣策略法来求解。对于B来讲,乙严格占优于甲,因此B肯定不会选择甲,于是剔除甲策略。在剩余的矩阵中,对于A来讲,β严格占优于α,所以A不会选择α,于是再剔除α策略。重复严格剔除劣策略后,矩阵变为:(1)分析如下:A选β时,B最优的选择是丙,因为8>6;A选γ时,B最优的选择是乙,因为9>8;B选乙时,A最优的选择是γ,因为10>7;B选丙时,A最优的选择是β,因为9>7。可得出(γ,乙),(β,丙)是纯策略均衡。(2)另外该博弈还有一个混合策略均衡,求解如下:设A以p的概率选择策略β,B以q的概率选择策略乙,则根据同等支付原则有:7q+9(1一q)=10q+8(1一q)6p+9(1一p)=8p+8(1一p)因此,是一个混合策略均衡,表示A以的概率选择β,的概率选择γ;B以的概率选择乙,的概率选择丙时,这个混合策略组合就构成了一个纳什均衡。
相似问题
一个垄断厂商面临两类消费者:学生和非学生。每个学生的需求函数为q=100一2p 每个非学生的需求函数
一个垄断厂商面临两类消费者:学生和非学生。每个学生的需求函数为q=100一2p,每个非学生的需求函数为q=100—p,市场上学生的数量为x,非学生数量为y,厂
一个垄断者在一个工厂中生产产品而在两个市场上销售。他的成本曲线和两个市场的需求曲线方程分别为:TC=
一个垄断者在一个工厂中生产产品而在两个市场上销售。他的成本曲线和两个市场的需求曲线方程分别为:TC=(Q1+Q2)2+10(Q1+Q2);Q1=32—0.4P1;Q2=18一0.1
如果在企业的短期均衡产量上 市场价格小于SAC 但高于AVC 那么企业( )。(上海财经大学2009
如果在企业的短期均衡产量上,市场价格小于SAC,但高于AVC,那么企业( )。(上海财经大学2009研)A.出现亏损,应立即停产B.亏损,但继续生产C.亏损,生
纳什均衡与占优策略的联系如何?(上海交通大学2006研)请帮忙给出正确答案和分析 谢谢!
纳什均衡与占优策略的联系如何?(上海交通大学2006研)请帮忙给出正确答案和分析,谢谢!
二级价格歧视的例子为( )。(上海财经大学2008研)A.供水部门根据水的消费量制定不同的价格B.航
二级价格歧视的例子为( )。(上海财经大学2008研)A.供水部门根据水的消费量制定不同的价格B.航空公司根据旅客的类型制定不同的价格C.企业根据消费者的












