判断I+J 是否正定矩阵 其中J是元素全为1的n级矩阵.请帮忙给出正确答案和分析 谢谢!
判断I+J,是否正定矩阵,其中J是元素全为1的n级矩阵.
请帮忙给出正确答案和分析,谢谢!
参考解答
正确答案:J是元素全为1的n级矩阵.J的顺序主子式1>0;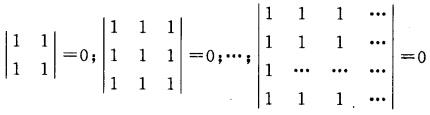 所以J为半正定矩阵又因为I是正定矩阵故由(13)题结论知I+J是正定矩阵.
所以J为半正定矩阵又因为I是正定矩阵故由(13)题结论知I+J是正定矩阵.
J是元素全为1的n级矩阵.J的顺序主子式1>0;所以J为半正定矩阵又因为I是正定矩阵,故由(13)题结论知I+J是正定矩阵.
相似问题
设函数f(x)在x0处可导 则f(x0)=( ).A.B.C.D.此题为多项选择题。请帮忙给出正确答
设函数f(x)在x0处可导,则f(x0)=( ).A.B.C.D.此题为多项选择题。请帮忙给出正确答案和分析,谢谢!
求y=x2 y=0 x=1分别绕x轴和y轴旋转所得的旋转体的体积.请帮忙给出正确答案和分析 谢谢!
求y=x2,y=0,x=1分别绕x轴和y轴旋转所得的旋转体的体积.请帮忙给出正确答案和分析,谢谢!
在平面S(点集)上定义一个二元关系:在平面S(点集)上定义一个二元关系:与Q位与同一条水平线上(与z
在平面S(点集)上定义一个二元关系:在平面S(点集)上定义一个二元关系:与Q位与同一条水平线上(与z在平面S(点集)上定义一个二元关系:与Q位与同一条水平线
如果A是n级正定矩阵 B是n级实对称矩阵 则存在一个N级实可逆矩阵C 使得CAC与CBC都是对角矩阵
如果A是n级正定矩阵,B是n级实对称矩阵,则存在一个N级实可逆矩阵C,使得CAC与CBC都是对角矩阵.请帮忙给出正确答案和分析,谢谢!
设y=(tan x)sin x;y=(tan x)sin x;请帮忙给出正确答案和分析 谢谢!
设y=(tan x)sin x;y=(tan x)sin x;请帮忙给出正确答案和分析,谢谢!












