如果A是n级正定矩阵 B是n级实对称矩阵 则存在一个N级实可逆矩阵C 使得CAC与CBC都是对角矩阵
如果A是n级正定矩阵，B是n级实对称矩阵，则存在一个N级实可逆矩阵C，使得CAC与CBC都是对角矩阵．
请帮忙给出正确答案和分析，谢谢！
参考解答
490***101
2024-11-13 10:25:34
正确答案：因为A是n级正定矩阵所以它与单位阵合同故存在实可逆矩阵D使得DTAD=I又因为B为实对称矩阵故DTBD仍为实对称的从而存在正交矩阵Q使
令C=DQ又因为QTQ=I所以CTAC=(DQ)TA(DQ)=QT(DTAD)Q—Q-1Q=I且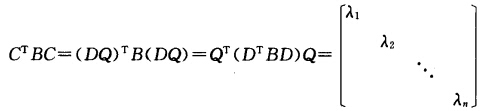
即存在可逆矩阵c使得CTAC与CTBC同时为对角矩阵．
因为A是n级正定矩阵,所以它与单位阵,合同,故存在实可逆矩阵D,使得DTAD=I,又因为B为实对称矩阵,故DTBD仍为实对称的,从而存在正交矩阵Q,使令C=DQ,又因为QTQ=I,所以CTAC=(DQ)TA(DQ)=QT(DTAD)Q—Q-1,Q=I且即存在可逆矩阵c使得CTAC与CTBC同时为对角矩阵．
相似问题
设y＝(tan x)sin x；y＝(tan x)sin x；请帮忙给出正确答案和分析 谢谢！
设y＝(tan x)sin x；y＝(tan x)sin x；请帮忙给出正确答案和分析，谢谢！
设ξ1 ξ2是任意两个随机变量 下面等式成立的是( )．A．E(ξ1＋ξ2)＝E(ξ1)＋E(ξ2)
设ξ1，ξ2是任意两个随机变量，下面等式成立的是( )．A．E(ξ1＋ξ2)＝E(ξ1)＋E(ξ2)B．D(ξ1＋ξ2)＝D(ξ1)＋D(ξ2)C．E(ξ1ξ2)＝E(ξ1)E(ξ2)D．有
求下列微分方程的解：y'＋3y＝2sin x．y'＋3y＝2sin x．请帮忙给出正确答案和分析 谢
求下列微分方程的解：y "＋3y＝2sin x．y "＋3y＝2sin x．请帮忙给出正确答案和分析，谢谢！
2)y'＋16y＝0 y(0)＝0 y(0)＝4．请帮忙给出正确答案和分析 谢谢！
2)y "＋16y＝0，y(0)＝0，y(0)＝4．请帮忙给出正确答案和分析，谢谢！
求下列各函数的二阶导数y'：y＝(1＋x2)arctan x；y＝(1＋x2)arctan x；请帮
求下列各函数的二阶导数y "：y＝(1＋x2)arctan x；y＝(1＋x2)arctan x；请帮忙给出正确答案和分析，谢谢！
