设n维行向量 矩阵A=E-αTα B=E+2αTα 其中E为n阶单位矩阵 则AB等于A.0.B.-E
设n维行向量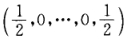 ,矩阵A=E-αTα,B=E+2αTα,其中E为n阶单位矩阵,则AB等于
,矩阵A=E-αTα,B=E+2αTα,其中E为n阶单位矩阵,则AB等于
A.0.
B.-E.
C.E.
D.E+αTα.
请帮忙给出正确答案和分析,谢谢!
参考解答
正确答案:C
相似问题
设an≤bn≤cn(n=1 2 …) 证明若收敛.请帮忙给出正确答案和分析 谢谢!
设an≤bn≤cn(n=1,2,…),证明若收敛.请帮忙给出正确答案和分析,谢谢!
已知函数f(x y)在点(0 0)的某个邻域内连续 且则( )。A.点(0 0)不是f(x y)的极
已知函数f(x,y)在点(0,0)的某个邻域内连续,且则( )。A.点(0,0)不是f(x,y)的极值点B.点(0,0)是f(x,y)的极大值点C.点(0,0)是f(x,y)的极小值点
已知f(x)在点戈=0的某个邻域内可展成泰勒级数 且则f'(0)=_____.请帮忙给出正确答案和分
已知f(x)在点戈=0的某个邻域内可展成泰勒级数,且则f "(0)=_____.请帮忙给出正确答案和分析,谢谢!
设n阶方阵A B C满足关系式ABC-E 其中E是n阶单位矩阵 则必有A.ACB=E.B.CBA=E
设n阶方阵A、B、C满足关系式ABC-E,其中E是n阶单位矩阵,则必有A.ACB=E.B.CBA=E.C.BAC=E.D.BcA=E.请帮忙给出正确答案和分析,谢谢!
已知y1=4n3 y2=3n2 y3=n是方程yn+2+a1(n)yn+1+a2(n)yn=f(n)
已知y1=4n3,y2=3n2,y3=n是方程yn+2+a1(n)yn+1+a2(n)yn=f(n)的三个特解,问它们能否组合构造出所给方程的通解;如可以,给出方程的通解.请帮忙












