已知函数f(u)具有二阶导数 且f(0)＝1 函数y＝y(x)由方程yxey－1＝1所确定 设z＝f
已知函数f(u)具有二阶导数，且f(0)＝1，函数y＝y(x)由方程yxey－1＝1所确定，设z＝f(lny—sinx)，求
。
请帮忙给出正确答案和分析，谢谢！
参考解答
4j8***101
2024-11-08 21:51:35
正确答案：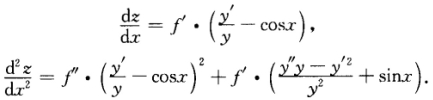
而由y—xeyy－1＝1两边对x求导得 y'－ey－1－xey－1y'＝0．再对x求导得 y'－ey－1y'－ey－1y'一xey－1y'－xey－1y'＝0．将x＝0y＝1代入上面两式得y'(0)＝1y'(0)＝2．故
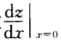＝f'(0)(0—0)＝0
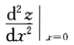f'(0).(2－1)＝1．
而由y—xeyy－1＝1两边对x求导得y'－ey－1－xey－1y'＝0．再对x求导得y'－ey－1y'－ey－1y'一xey－1y'－xey－1y'＝0．将x＝0,y＝1代入上面两式得y'(0)＝1,y'(0)＝2．故＝f'(0)(0—0)＝0,f'(0).(2－1)＝1．
相似问题
已知点A(2 1 4) B(4 3 10) 写出以线段AB为直径的球面方程．请帮忙给出正确答案和分析
已知点A(2，1，4)、B(4，3，10)，写出以线段AB为直径的球面方程．请帮忙给出正确答案和分析，谢谢！
设准线方程为 母线的方向向量为｛－1 0 1｝ 求该柱面方程．请帮忙给出正确答案和分析 谢谢！
设准线方程为，母线的方向向量为｛－1，0，1｝，求该柱面方程．请帮忙给出正确答案和分析，谢谢！
已知函数z＝f(x y)的全微分dz＝2xdx－2ydy 并且f(1 1)＝2．求f(x y)在椭圆
已知函数z＝f(x，y)的全微分dz＝2xdx－2ydy，并且f(1，1)＝2．求f(x，y)在椭圆域上的最大值和最小值．请帮忙给出正确答案和分析，谢谢！
题4已知A与B的直角坐标分别为(1 0 0)与(0 1 1) 线段AB绕x轴旋转一周所成的旋转曲面为
题4已知A与B的直角坐标分别为(1，0，0)与(0，1，1)，线段AB绕x轴旋转一周所成的旋转曲面为s，求由S及两平面z＝0，z＝1所围成的立体体积．请帮忙给出正确
已知z＝uv 求dz．请帮忙给出正确答案和分析 谢谢！
已知z＝uv，，求dz．请帮忙给出正确答案和分析，谢谢！
