已知函数z＝f(x y)的全微分dz＝2xdx－2ydy 并且f(1 1)＝2．求f(x y)在椭圆
已知函数z＝f(x，y)的全微分dz＝2xdx－2ydy，并且f(1，1)＝2．求f(x，y)在椭圆域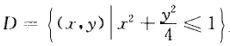
上的最大值和最小值．
请帮忙给出正确答案和分析，谢谢！
参考解答
473***101
2024-11-08 21:26:26
正确答案：[详解1 由dz＝2xdx－2ydy可知 z＝f(xy)＝＝x2＋y2＋C．由f(11)＝2得C＝2故 z＝f(xy)＝x2－y2＋2．令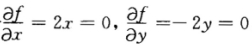
解得驻点(00)．在椭圆
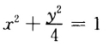上z＝x2－(4—4x2)＋2即 z＝5x2－2(－1≤x≤1)其最大值为
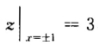最小值为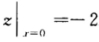
再与f(00)＝2比较可
[分析先由全微分的表达式求出f(x，y)的表达式，再求其最值．[评注此题的新颖点在于要求极值的函数没有直接给出，需要根据全微分的表达式求出后再讨论其最值．
相似问题
题4已知A与B的直角坐标分别为(1 0 0)与(0 1 1) 线段AB绕x轴旋转一周所成的旋转曲面为
题4已知A与B的直角坐标分别为(1，0，0)与(0，1，1)，线段AB绕x轴旋转一周所成的旋转曲面为s，求由S及两平面z＝0，z＝1所围成的立体体积．请帮忙给出正确
已知z＝uv 求dz．请帮忙给出正确答案和分析 谢谢！
已知z＝uv，，求dz．请帮忙给出正确答案和分析，谢谢！
已知xy＝xf(z)＋yg(z) xf(z)＋yg(2)≠0 其中z＝z(x y)是x和y的函数 求
已知xy＝xf(z)＋yg(z)，xf(z)＋yg(2)≠0，其中z＝z(x，y)是x和y的函数，求证： ．请帮忙给出正确答案和分析，谢谢！
某养殖厂饲养两种鱼 若甲种鱼放养x(万尾) 乙种鱼放养y(万尾) 收获时两种鱼的收获量分别为 (3－
某养殖厂饲养两种鱼，若甲种鱼放养x(万尾)，乙种鱼放养y(万尾)，收获时两种鱼的收获量分别为 (3－αx－βy)x和(4－βx－2ay)y(α＞β＞0)， 求使得产鱼
过点Po(xo yo zo)分别作平行于z轴的直线和平行于xOy面的平面 问在它们上面的点的坐标各有
过点Po(xo，yo，zo)分别作平行于z轴的直线和平行于xOy面的平面，问在它们上面的点的坐标各有什么特征?请帮忙给出正确答案和分析，谢谢！
