讨论下列随机变量的数学期望和方差是否存在： (1)随机变量X的分布律为 2)随机变量X的概率密度为
讨论下列随机变量的数学期望和方差是否存在： (1)随机变量X的分布律为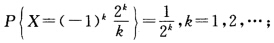 
2)随机变量X的概率密度为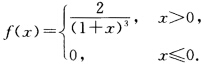 
请帮忙给出正确答案和分析，谢谢！
参考解答
4j5***444
2023-11-13 23:21:41
正确答案：(1)对离散型随机变量X如果它的分布律为P{X=xk=pkk=12…由数学期望的定义．当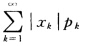
收敛时数学期望E(X)存在．这里由于
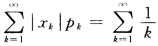是调和级数发散故X的数学期望不存在因而方差也不存在． (2)对连续型随机变量X如果它的概率密度为f(x)由数学期望的定义．当∫—∞+∞｜x｜f(x)dx收敛时数学期望E(X)存在．这里由于
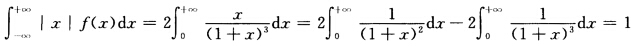收敛故E(X)存在．然而
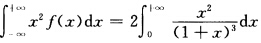发散故方差不存在．
(1)对离散型随机变量X,如果它的分布律为P{X=xk=pk,k=1,2,…,由数学期望的定义．当收敛时,数学期望E(X)存在．这里由于是调和级数,发散,故X的数学期望不存在,因而方差也不存在．(2)对连续型随机变量X,如果它的概率密度为f(x),由数学期望的定义．当∫—∞+∞｜x｜f(x)dx收敛时,数学期望E(X)存在．这里由于收敛,故E(X)存在．然而,发散,故方差不存在．
相似问题
设二维随机变量(X Y)的概率密度为 求：①条件概率密度； ②在X=的条件下 Y的条件分布函数。请
设二维随机变量(X，Y)的概率密度为 求：①条件概率密度； ②在X=的条件下，Y的条件分布函数。请帮忙给出正确答案和分析，谢谢！
设(X Y)服从二维正态分布 X=X+2Y Y=X一2Y 则X Y不相关的充要条件是( )．A．D(
设(X，Y)服从二维正态分布，X=X+2Y，Y=X一2Y，则X，Y不相关的充要条件是( )．A．D(X)=D(Y)B．D(X)=2D(Y)C．D(X)=3D(Y)D．D(X)=4D(Y)请帮忙给出正确答案和分析，谢谢！
设有随机过程X(t)=Vt+b t∈(0 +∞) b为常数 V～N(0 1) 求X(t)的一维分布密
设有随机过程X(t)=Vt+b，t∈(0，+∞)，b为常数，V～N(0，1)，求X(t)的一维分布密度、均值和相关函数．请帮忙给出正确答案和分析，谢谢！
设随机变量X的概率密度为 当X=x(x＞0)时 Y的条件概率密度为 求：(X Y)的概率密度f(
设随机变量X的概率密度为 当X=x(x＞0)时，Y的条件概率密度为 求：(X，Y)的概率密度f(x，y)，P{X—y＞1}．请帮忙给出正确答案和分析，谢谢！
设随机变量(X Y)的分布律为 且P{X—y}= 则( )． 请帮忙给出正确答案和分析 谢谢！
设随机变量(X，Y)的分布律为 且P{X—y}=，则( )． 请帮忙给出正确答案和分析，谢谢！
