用高斯定理解题的步骤及可解性条件是什么?请帮忙给出正确答案和分析 谢谢！

正确答案：应用高斯定理解题的步骤如下： (1)进行对称性分析大学物理中常见的对称性有球对称性即均匀带电球面、球体、球壳或多层球壳等；轴对称性即均匀带电无限长直线、圆柱体、圆柱面或同轴圆柱面等；面对称性即均匀带电无限大平面、平板、平行平板等。 (2)选取适当的高斯面使穿过高斯面的电通量易于计算。高斯面上电场强度不变。 (3)计算高斯面上穿过的电通量和高斯面内包围的电量的代数和列方程求解。 应用高斯定理由直接积分法求解电场强度可解的条件是以E为变量的积分方程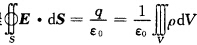可解的条件。要求出E的大小或者某分量则包含电场强度E的大小或其某分量的被积函数必可提到积分号外从而可求出电场强度E。 首先分析电荷分布的对称性特点以及电力线垂直等势面的特点；选取适当的高斯面再将二重积分化为一重积分要使二重积分能化为一重积分且只包含E的某一分量电场强度的方向必沿某个曲线坐标线的方向并且高斯面由分片光滑坐标面(或一部分)构成。在高斯面．(或一部分)上通量积分可简化为一重积分若再能由电荷或电势及电场强度的对称性判定一重积分的被积函数为常数。而其余高斯面(如果存在)上电通量为零电场强度E的大小在高斯面上不变的情况是上面的特例。据此可知有限长均匀带电直线带电导体圆盘等都是可解的。
应用高斯定理解题的步骤如下：(1)进行对称性分析,大学物理中常见的对称性有球对称性,即均匀带电球面、球体、球壳或多层球壳等；轴对称性,即均匀带电无限长直线、圆柱体、圆柱面或同轴圆柱面等；面对称性,即均匀带电无限大平面、平板、平行平板等。(2)选取适当的高斯面,使穿过高斯面的电通量易于计算。高斯面上电场强度不变。(3)计算高斯面上穿过的电通量和高斯面内包围的电量的代数和,列方程求解。应用高斯定理由直接积分法求解电场强度,可解的条件是以E为变量的积分方程可解的条件。要求出E的大小或者某分量,则包含电场强度E的大小或其某分量的被积函数必可提到积分号外,从而可求出电场强度E。首先分析电荷分布的对称性特点,以及电力线垂直等势面的特点；选取适当的高斯面,再将二重积分化为一重积分,要使二重积分能化为一重积分且只包含E的某一分量,电场强度的方向必沿某个曲线坐标线的方向,并且高斯面由分片光滑坐标面(或一部分)构成。在高斯面．(或一部分)上,通量积分可简化为一重积分,若再能由电荷或电势及电场强度的对称性判定一重积分的被积函数为常数。而其余高斯面(如果存在)上电通量为零,电场强度E的大小在高斯面上不变的情况是上面的特例。据此可知有限长均匀带电直线,带电导体圆盘等都是可解的。