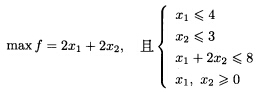
参考解答
正确答案:我们在直角坐标系中进行求解。(1)建立x2Ox2直角坐标系见图1.8所示。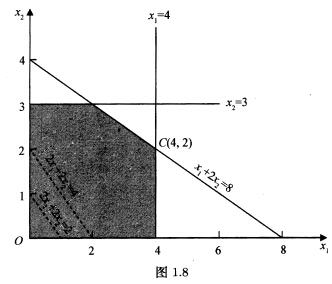 (2)求满足线性规划问题约束条件中的可行域。将满足约束条件的区域画出来。该区域成为可行域例如在图1.8中阴影部分即为可行域。(3)求目标函数的最优解。要求目标函数f=2x1+2x2达到最大值的点。为此我们可以考虑以常数d为参数的直线fd:2x1+2x2=d。对不同的d值在直角坐标系的平面上可描绘出一组平行的直线因此我们可以根据d的不同取值通过观察即可直接判断目标函数的变化趋势进而获得目标函数的最优解。(i)d取不同的值42即:令目标函数2x1+2x2=4或2x1+2x2=2。斜率已知显然不是最大值。(ii)平行移动上述直线方向按法线方向(高度增加的方向)到C点为止C(42)。最优解x1=4x2=2最优值:2x1+2x2=12若求最小按法线方向向下移动。
(2)求满足线性规划问题约束条件中的可行域。将满足约束条件的区域画出来。该区域成为可行域例如在图1.8中阴影部分即为可行域。(3)求目标函数的最优解。要求目标函数f=2x1+2x2达到最大值的点。为此我们可以考虑以常数d为参数的直线fd:2x1+2x2=d。对不同的d值在直角坐标系的平面上可描绘出一组平行的直线因此我们可以根据d的不同取值通过观察即可直接判断目标函数的变化趋势进而获得目标函数的最优解。(i)d取不同的值42即:令目标函数2x1+2x2=4或2x1+2x2=2。斜率已知显然不是最大值。(ii)平行移动上述直线方向按法线方向(高度增加的方向)到C点为止C(42)。最优解x1=4x2=2最优值:2x1+2x2=12若求最小按法线方向向下移动。
我们在直角坐标系中进行求解。(1)建立x2Ox2直角坐标系,见图1.8所示。(2)求满足线性规划问题约束条件中的可行域。将满足约束条件的区域画出来。该区域成为可行域,例如在图1.8中阴影部分,即为可行域。(3)求目标函数的最优解。要求目标函数f=2x1+2x2达到最大值的点。为此我们可以考虑以常数d为参数的直线fd:2x1+2x2=d。对不同的d值,在直角坐标系的平面上可描绘出一组平行的直线,因此,我们可以根据d的不同取值,通过观察即可直接判断目标函数的变化趋势,进而获得目标函数的最优解。(i)d取不同的值4,2,即:令目标函数2x1+2x2=4或2x1+2x2=2。斜率已知,显然不是最大值。(ii)平行移动上述直线,方向按法线方向(高度增加的方向)到C点为止,C(4,2)。最优解x1=4,x2=2最优值:2x1+2x2=12若求最小,按法线方向向下移动。
相似问题
函数μ=eaχ(0<χ<∞)的归一化因子c等于何值?请帮忙给出正确答案和分析 谢谢!
函数μ=eaχ(0<χ<∞)的归一化因子c等于何值?请帮忙给出正确答案和分析,谢谢!
某工厂在计划期内安排生产两种产品Ⅰ Ⅱ 已知生产单位产品所需的设备台时及A B两种原材料的消耗情况
某工厂在计划期内安排生产两种产品Ⅰ,Ⅱ,已知生产单位产品所需的设备台时及A,B两种原材料的消耗情况,如表3.13所示。 该厂每生产一件产品I可获利2
求H原子的轨道上的电子出现在θ=45°的圆锥内的概率。 请帮忙给出正确答案和分析 谢谢!
求H原子的轨道上的电子出现在θ=45°的圆锥内的概率。 请帮忙给出正确答案和分析,谢谢!
设有4件工作分派给4个人来做 每项工作只能由一个人来做 每个人只能做一项工作。表6.7为各人对各项工
设有4件工作分派给4个人来做,每项工作只能由一个人来做,每个人只能做一项工作。表6.7为各人对各项工作所具有的工作效率,请适当安排人选,使总效率最
如何理解非金属性的强弱?请帮忙给出正确答案和分析 谢谢!
如何理解非金属性的强弱?请帮忙给出正确答案和分析,谢谢!