设un≠0(n=1 2 3…) 且则级数( ).A.发散B.绝对收敛C.条件收敛D.收敛性根据所给条
设un≠0(n=1,2,3…),且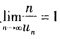 则级数
则级数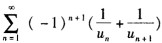 ( ).
( ).
A.发散
B.绝对收敛
C.条件收敛
D.收敛性根据所给条件不能判定
请帮忙给出正确答案和分析,谢谢!
参考解答
正确答案:C
因为所以原级数收敛,故排除A、D.又由n→∞时un=n(1+an)知,当n充分大时,un>0且而发散,因此级数发散,从而原级数条件收敛.
相似问题
下列说法中正确的是( ).A.若z=f(x y)在M0点任一方向的方向导数都存在 则z在该点存在偏导
下列说法中正确的是( ).A.若z=f(x,y)在M0点任一方向的方向导数都存在,则z在该点存在偏导数B.若z=f(x,y)在M0点可微,则它在M0点的一阶偏导数连续C
设数列{an} 其中an≠0(n=1 2 …) 且此题为判断题(对 错)。请帮忙给出正确答案和分析
设数列{an},其中an≠0(n=1,2,…),且此题为判断题(对,错)。请帮忙给出正确答案和分析,谢谢!
求级数讨论下列级数的敛散性:讨论下列级数的敛散性: 请帮忙给出正确答案和分析 谢谢!
求级数讨论下列级数的敛散性:讨论下列级数的敛散性: 请帮忙给出正确答案和分析,谢谢!
利用积分判断法 判别下列级数的敛散性: 此题为判断题(对 错)。请帮忙给出正确答案和分析 谢谢!
利用积分判断法,判别下列级数的敛散性: 此题为判断题(对,错)。请帮忙给出正确答案和分析,谢谢!
设函数y=f(x)具有二阶导数 且f(x)>0 f'(x)>0 △x为自变量x在点x0处的增量 △y
设函数y=f(x)具有二阶导数,且f(x)>0,f"(x)>0,△x为自变量x在点x0处的增量,△y与dy分别为f(x)在点x0处对应的增量与微分,若△x>0,则( ).A.0<dy<△












