已知f(x)是连续函数 证明:求由曲线y=lnx与直线y=lnx及y=lnb所围图形的面积(b>a>
已知f(x)是连续函数,证明:求由曲线y=lnx与直线y=lnx及y=lnb所围图形的面积(b>a>0).
求由曲线y=lnx与直线y=lnx及y=lnb所围图形的面积(b>a>0).
请帮忙给出正确答案和分析,谢谢!
参考解答
正确答案: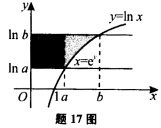 如题17图若以x为积分变量则需计算两块图形面积之和因此改为以y为积分变量.于是所求面积
如题17图若以x为积分变量则需计算两块图形面积之和因此改为以y为积分变量.于是所求面积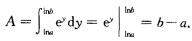
如题17图,若以x为积分变量,则需计算两块图形面积之和,因此改为以y为积分变量.于是所求面积
相似问题
分析函数y=arctancose2x是由哪些函数复合而成.请帮忙给出正确答案和分析 谢谢!
分析函数y=arctancose2x是由哪些函数复合而成.请帮忙给出正确答案和分析,谢谢!
证明不等式利用定积分的几何意义 说明下列等式:(1)利用定积分的几何意义 说明下列等式:(1)请帮忙
证明不等式利用定积分的几何意义,说明下列等式:(1)利用定积分的几何意义,说明下列等式:(1)请帮忙给出正确答案和分析,谢谢!
已知讨论极限是否存在.讨论极限是否存在.请帮忙给出正确答案和分析 谢谢!
已知讨论极限是否存在.讨论极限是否存在.请帮忙给出正确答案和分析,谢谢!
某物价指数由三种商品价格构成 其比重依次为0.4 0.3 0.3 设三种商品价格上涨的可能性依次为0
某物价指数由三种商品价格构成,其比重依次为0.4,0.3,0.3,设三种商品价格上涨的可能性依次为0.6,0.8,0.5.试求:求该物价指数上涨的概率;请
假定f是连续的 而且请帮忙给出正确答案和分析 谢谢!
假定f是连续的,而且请帮忙给出正确答案和分析,谢谢!












