已知半径为R 质量为M表面光滑的半球放在光滑水平面上 在其顶点上放置一个质量为m(m<M)的小滑块
已知半径为R,质量为M表面光滑的半球放在光滑水平面上,在其顶点上放置一个质量为m(m<M)的小滑块,初速为零释放使其运动。求小滑块脱离半球时,图1—28所示的θ角等于多少? 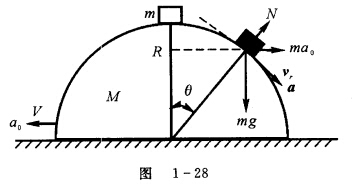
请帮忙给出正确答案和分析,谢谢!
参考解答
正确答案:当小滑块和半球脱离时两者间的作用力为零。此时半球仅受重力和支持力二力平衡即a0=0。此时小滑块相对半球面作圆周运动以半球为参考系由牛顿第二定律得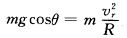 即 vr2=gRcosθ 选以小滑块和半球脱离时半球的速度V运动的物体为惯性参考系则系统水平方向动量守恒(m+M)V=mvrcosθ式中V为小滑块和半球初始时刻的相对速度。 从初态到末态的过程中一对支持力及地面支持力不做功重力为保守力选脱离点为势能零点由机械能守恒
即 vr2=gRcosθ 选以小滑块和半球脱离时半球的速度V运动的物体为惯性参考系则系统水平方向动量守恒(m+M)V=mvrcosθ式中V为小滑块和半球初始时刻的相对速度。 从初态到末态的过程中一对支持力及地面支持力不做功重力为保守力选脱离点为势能零点由机械能守恒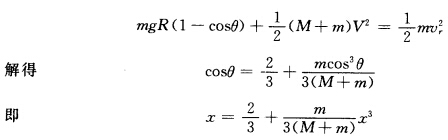 令
令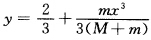 则
则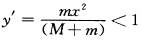 吸引流域为
吸引流域为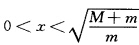 由压缩映射知存在不动点。在吸引流域内取初值x=cosθ=
由压缩映射知存在不动点。在吸引流域内取初值x=cosθ=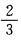 迭代几次即得不动点一级近似解为
迭代几次即得不动点一级近似解为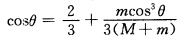
当小滑块和半球脱离时,两者间的作用力为零。此时半球仅受重力和支持力,二力平衡,即a0=0。此时小滑块相对半球面作圆周运动,以半球为参考系,由牛顿第二定律得即vr2=gRcosθ选以小滑块和半球脱离时半球的速度V运动的物体为惯性参考系,则系统水平方向动量守恒,(m+M)V=mvrcosθ,式中V为小滑块和半球初始时刻的相对速度。从初态到末态的过程中一对支持力及地面支持力不做功,重力为保守力,选脱离点为势能零点,由机械能守恒令,则吸引流域为由压缩映射知,存在不动点。在吸引流域内取初值x=cosθ=迭代几次即得不动点,一级近似解为
相似问题
如何将二体问题化为单体问题?请帮忙给出正确答案和分析 谢谢!
如何将二体问题化为单体问题?请帮忙给出正确答案和分析,谢谢!
证明不可约矩阵不可能有零行或零列.请帮忙给出正确答案和分析 谢谢!
证明不可约矩阵不可能有零行或零列.请帮忙给出正确答案和分析,谢谢!
设A为不可约随机矩阵 则存在的充分必要条件是A为素矩阵.请帮忙给出正确答案和分析 谢谢!
设A为不可约随机矩阵,则存在的充分必要条件是A为素矩阵.请帮忙给出正确答案和分析,谢谢!
设P-1AP=A 其中.求A11.请帮忙给出正确答案和分析 谢谢!
设P-1AP=A,其中.求A11.请帮忙给出正确答案和分析,谢谢!
计算下列乘积: 请帮忙给出正确答案和分析 谢谢!
计算下列乘积: 请帮忙给出正确答案和分析,谢谢!












