一个点电荷q位于内 外半径分别为R1和R2 带电量为Q的金属球壳的球心处。求：（1）球壳内 外表面上

正确答案：（1）由于球壳处于点电荷q产生的静电场内故将产生静电感应现象。达到静电平衡时应满足静电平衡条件。即球壳内电场强度为零电荷只分布在球壳的表面。又由点电荷的电场强度的球对称性和球壳内、外表面上任意一点的曲率分别相等可知电荷在球壳的内、外表面的分布是均匀的。设球壳内、外表面所带的电量分别为q₁和q₂。在球壳内任意做一个闭合曲面作为高斯面则通过该闭合曲面的电通量为零。由高斯定理可知闭合曲面内包围的电荷电量的代数和为零。即q＋q₁＝0因而得到球壳内表面分布的电荷量值为q₁＝－q （1）由电荷守恒定律q₁＋q₂＝Q可得球壳外表面的电荷量为q₂＝Q＋q （2）（2）由式（1）可知电荷分布具有球对称性故电场分布也具有球对称性。以任意长r为半径做一个球面为高斯面则通过所作球面的电通量为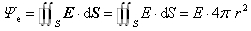 （3）导体球壳内（r＜R₁）球面包围的电荷为q。由高斯定理可得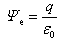(4）联立求解式（3）和（4）可得 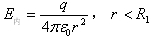导体球壳里（R＜r＜R₂）由导体的静电平衡条件可得E_里=0R＜r＜R₂导体球壳外（r＞R₂）球面包围的电荷代数和为Q＋q。由高斯定理可得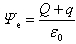（5）联立求解式（3）和（5）可得 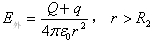（3）由电势的定义U=∫_p^p₀E.dl=∫_p^∞E.dl可得导体球壳内任意一点（r＜R₁）的电势为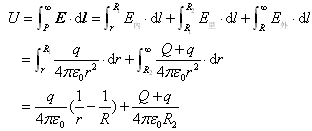导体球壳里面任意一点（R₁＜r＜R₂）的电势U=∫_p^∞E.dl= 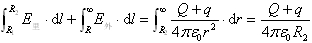导体球外任意一点（r＞R₂）的电势U=∫_p^∞E.dl =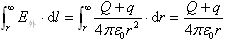
（1）由于球壳处于点电荷q产生的静电场内,故将产生静电感应现象。达到静电平衡时,应满足静电平衡条件。即球壳内电场强度为零,电荷只分布在球壳的表面。又由点电荷的电场强度的球对称性和球壳内、外表面上任意一点的曲率分别相等,可知电荷在球壳的内、外表面的分布是均匀的。设球壳内、外表面所带的电量分别为q1和q2。在球壳内任意做一个闭合曲面作为高斯面,则通过该闭合曲面的电通量为零。由高斯定理可知,闭合曲面内包围的电荷电量的代数和为零。即q＋q1＝0,因而得到球壳内表面分布的电荷量值为q1＝－q（1）由电荷守恒定律q1＋q2＝Q可得,球壳外表面的电荷量为q2＝Q＋q（2）（2）由式（1）可知,电荷分布具有球对称性,故电场分布也具有球对称性。以任意长r为半径做一个球面为高斯面,则通过所作球面的电通量为（3）导体球壳内（r＜R1）,球面包围的电荷为q。由高斯定理可得(4）联立求解式（3）和（4）可得导体球壳里（R＜r＜R2）,由导体的静电平衡条件可得E里=0,R＜r＜R2导体球壳外（r＞R2）,球面包围的电荷代数和为Q＋q。由高斯定理可得（5）联立求解式（3）和（5）可得（3）由电势的定义U=∫pp0E.dl=∫p∞E.dl,可得导体球壳内任意一点（r＜R1）的电势为导体球壳里面任意一点（R1＜r＜R2）的电势U=∫p∞E.dl=导体球外任意一点（r＞R2）的电势U=∫p∞E.dl=