如图17-1所示 三种载流导线在平面内分布 电流强度均为I 求它们各在点O的磁感应强度的大小和方向。

正确答案：（a）载流导线可以视为由两个载流“半无限长”直导线和半径为R的载流圆环导线组合而成的。两半无限长直导线在点O产生的磁感应强度叠加等效于一个载流无限长直导线在点O（距导线为R）处产生的磁感应强度其大小为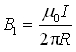（1）方向垂直纸面向外。在缺口可以忽略的情况下半径为R的载流圆环导线(圆环电流)产生的磁感应强度就相当于一个的圆环电流在圆心处的磁感应强度其大小为 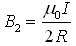（2）方向垂直纸面向里。根据叠加原理点O处总磁感应强度其大小为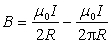方向垂直纸面向里。（b）载流导线可以视为由两个“半无限长”直电流和半径为R的四分之一圆环电流组合而成的。两直线电流的延长线过点O故它们在点O不产生磁感应强度。由于圆环电流为圆周的1/4故它在点O的磁感应强度为圆电流的磁感应强度的1/4。因而点O的磁感应强度的大小为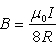方向垂直纸面向里。（c）正方形载流导线可以视为由四根长度为L的直电流组合而成的。点O到每一边（直电流）的距离均为L/2导线上电流流入端和流出端对点O的张角分别为45°和135°。一根直导线在点O的磁感应强度大小为 （1）方向垂直纸面向外。整个正方形电流产生的磁感应强度方向相同根据叠加原理总磁感应强度大小为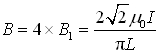方向垂直纸面向外。
（a）载流导线可以视为由两个载流“半无限长”直导线和半径为R的载流圆环导线组合而成的。两半无限长直导线在点O产生的磁感应强度叠加,等效于一个载流无限长直导线在点O（距导线为R）处产生的磁感应强度,其大小为（1）方向垂直纸面向外。在缺口可以忽略的情况下,半径为R的载流圆环导线(圆环电流)产生的磁感应强度就相当于一个的圆环电流在圆心处的磁感应强度,其大小为（2）方向垂直纸面向里。根据叠加原理,点O处总磁感应强度其大小为方向垂直纸面向里。（b）载流导线可以视为由两个“半无限长”直电流和半径为R的四分之一圆环电流组合而成的。两直线电流的延长线过点O,故它们在点O不产生磁感应强度。由于圆环电流为圆周的1/4,故它在点O的磁感应强度为圆电流的磁感应强度的1/4。因而点O的磁感应强度的大小为方向垂直纸面向里。（c）正方形载流导线可以视为由四根长度为L的直电流组合而成的。点O到每一边（直电流）的距离均为L/2,导线上电流流入端和流出端对点O的张角分别为45°和135°。一根直导线在点O的磁感应强度大小为（1）方向垂直纸面向外。整个正方形电流产生的磁感应强度方向相同,根据叠加原理,总磁感应强度大小为方向垂直纸面向外。