已知已知方阵A满足A2一A一2E=0 则A-1=_____ (A+2E)-1=_____.已知方阵A
已知已知方阵A满足A2一A一2E=0,则A-1=_____,(A+2E)-1=_____.
已知方阵A满足A2一A一2E=0,则A-1=_____,(A+2E)-1=_____.
请帮忙给出正确答案和分析,谢谢!
参考解答
正确答案: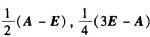
由A2一A一2E=O得A(A—E)=2E,即,故A是可逆,且A-1=(A—E).为了求(A+2E)-1,找矩阵B,使(A+2E)B=E,则(A+2E)-1=B由于故
相似问题
A B为n阶矩阵 且(A一B)2=E。则(层一AB-1)-1( ).A.B(A一B)B.一B(A一B
A、B为n阶矩阵,且(A一B)2=E。则(层一AB-1)-1( ).A.B(A一B)B.一B(A一B)C.B一(A一B)D.(A一B)B-1请帮忙给出正确答案和分析,谢谢!
设A B均为n阶方阵 则结论正确的是( ).A.A或B可逆 必有AB可逆B.A或B不可逆 必有AB不
设A,B均为n阶方阵,则结论正确的是( ).A.A或B可逆,必有AB可逆B.A或B不可逆,必有AB不可逆C.A、B均可逆,必有A+B可逆D.A、B均不可逆,必有A+B可逆
设A=(aij)为3阶非零实矩阵 且已知Aij=aij(其中Aij为aij的代数余子式) i j=1
设A=(aij)为3阶非零实矩阵,且已知Aij=aij(其中Aij为aij的代数余子式),i,j=1,2,3.证明:A可逆,并求|A|与A-1.请帮忙给出正确答案和分析,谢谢!
设4阶方阵A=设A= 其中ai≠0 bi≠0(i=1 2 … n) 则矩阵A的秩为r(A)=____
设4阶方阵A=设A=,其中ai≠0,bi≠0(i=1,2,…,n),则矩阵A的秩为r(A)=_______.设A=,其中ai≠0,bi≠0(i=1,2,…,n),则矩阵A的秩为r(A)=__
设A为n阶可逆矩阵 则下列结论正确的是( ).A.(2A)-1=2A-1B.(2A)T=2ATC.[
设A为n阶可逆矩阵,则下列结论正确的是( ).A.(2A)-1=2A-1B.(2A)T=2ATC.[(A-1)-1]T=[(AT)T]-1D. [(AT)-1]T=[(A-1)T]-1请帮忙给出正确答案和分析,谢谢!












