在平面S(点集)上定义一个二元关系： 证明：～是S上的一个等价关系．请帮忙给出正确答案和分析 谢谢！

正确答案：(1)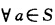显然a～a成立(反身性)．(2)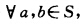若a～b即a_x一b_x∈Z且a_y一b_y∈Z则b_x一a_x=一(a_x一b_x)∈Zb_y一a_y=(a_y一b_y)∈Z成立即b～a．(对称性)．(3)S集中的任意3个二元关系a(xy)b(xy)c(xy)若a～b且b～c即有：(a_x一b_x)∈Z(b_x一c_x)∈Z则a_x一c_x=(a_x一b_x)+(b_x一c_x)∈z同理：a_y一c_y=(a_y一b_y)+(b_y一c_y)∈Z所以：a～c(传递性)．由(1)(2)(3)知满足等价关系成立条件．所以～是S上的一个等价关系．
(1),显然a～a,成立(反身性)．(2)若a～b,即ax一bx∈Z,且ay一by∈Z则bx一ax=一(ax一bx)∈Zby一ay=(ay一by)∈Z成立,即b～a．(对称性)．(3)S集中的任意3个二元关系,a(x,y),b(x,y),c(x,y)若a～b,且b～c,即有：(ax一bx)∈Z,(bx一cx)∈Z,则ax一cx=(ax一bx)+(bx一cx)∈z,同理：ay一cy=(ay一by)+(by一cy)∈Z,所以：a～c(传递性)．由(1),(2),(3)知满足等价关系成立条件．所以,～是S上的一个等价关系．