证明C—K方程P(n+m)=P(n)P(m)．请帮忙给出正确答案和分析 谢谢！

正确答案：这只需证明P⁽ⁿ⁾=PP^(n—1)即可．事实上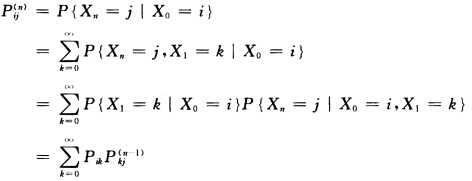从而可得P⁽ⁿ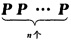⁾=即n步转移概率可由一步转移概率求出值得指出的是转移概率P_ij不包含初始分布亦即X₀—i的概率不能由转移概率P_ij表达因此过程还需有初始分布．令 p_i=P{X₀=i(i∈E)其中E为过程的状态空间称{p_i)(i∈E)为过程的初始分布其显然满足 p_i≥0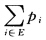=1 这样一个马尔可夫链的联合概率分布就可以由{p_i(i∈E)和其一步转移概率矩阵P完全决定．
这只需证明P(n)=PP(n—1)即可．事实上从而可得P(n)=,即n步转移概率可由一步转移概率求出,值得指出的是,转移概率Pij不包含初始分布,亦即X0—i的概率不能由转移概率Pij表达,因此过程还需有初始分布．令pi=P{X0=i(i∈E)其中E为过程的状态空间,称{pi)(i∈E)为过程的初始分布,其显然满足pi≥0,=1,这样,一个马尔可夫链的联合概率分布就可以由{pi(i∈E)和其一步转移概率矩阵P完全决定．