设状态连续 时间离散的随机过程X(t)=sin 2παt 其中t=1 2 … α服从(0 1)上均匀
设状态连续、时间离散的随机过程X(t)=sin 2παt，其中t=1，2，…，α服从(0，1)上均匀分布的随机变量，试讨论X(t)的平稳性．
请帮忙给出正确答案和分析，谢谢！
参考解答
42j***443
2023-11-13 13:54:07
正确答案：α的分布密度为 
所以 E[x(t)=E(sin 2παt)=∫—∞+∞sin 2πxtf(x)dx =∫01sin 2πtxdx=0CX(tt+τ)=RX(tt+τ)=E[X(t)X(t+τ)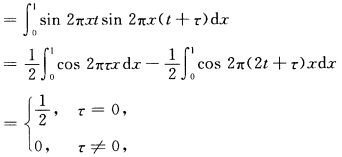
故{X(t)为平稳过程．
α的分布密度为所以E[x(t)=E(sin2παt)=∫—∞+∞sin2πxtf(x)dx=∫01sin2πtxdx=0,CX(t,t+τ)=RX(t,t+τ)=E[X(t)X(t+τ)故{X(t)为平稳过程．
相似问题
郑和下西洋是在哪个朝代?()A.唐代B.宋代C.明代D.清代
郑和下西洋是在哪个朝代?()A 唐代B 宋代C 明代D 清代
重复掷币一直到连续出现两次正面为止．假定钱币是均匀的 试引入以连续出现次数为状态空间的马尔可夫链 并
重复掷币一直到连续出现两次正面为止．假定钱币是均匀的，试引入以连续出现次数为状态空间的马尔可夫链，并求出平均需要掷多少次试验才可以结束．请帮忙
考虑一随机过程X(t) 自相关函数为RX(τ) 功率谱密度为SX(ω) 若SX(ω)=0 ｜ω｜＞ω
考虑一随机过程X(t)，自相关函数为RX(τ)，功率谱密度为SX(ω)，若SX(ω)=0，｜ω｜＞ω0，证明： 请帮忙给出正确答案和分析，谢谢！
设马尔可夫链的状态空间E={1 2 3 4) 其状态转移图如图6．2所示 研究其状态并判断其是否具有
设马尔可夫链的状态空间E={1，2，3，4)，其状态转移图如图6．2所示，研究其状态并判断其是否具有遍历性． 请帮忙给出正确答案和分析，谢谢！
A B两罐总共装着N个球 做如下试验：在时刻n先从N个球中等概率地任取一球；然后从A B两罐中任选一
A，B两罐总共装着N个球，做如下试验：在时刻n先从N个球中等概率地任取一球；然后从A，B两罐中任选一个，选中A的概率为p，选中B的概率为q；之后再将选出的
