证明：任意一条不通过完全四点形顶点的直线与完全四点形的三对对边的交点 是属于同一对合的三对对应点．(
证明：任意一条不通过完全四点形顶点的直线与完全四点形的三对对边的交点，是属于同一对合的三对对应点．(称为德萨格对合定理)．
请帮忙给出正确答案和分析，谢谢！
参考解答
473***102
2024-11-20 00:19:41
正确答案：如图2—3—11．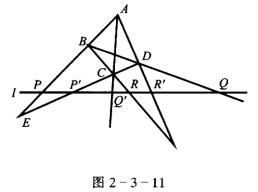
直线l与完全四点形ABCD的三对对边的交点为PP′；Q(C)Q′；RR′．在l上P→P′Q→Q′R→R′因为(PP′Q′R)
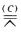(PEAB)
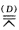(PP′R′Q)所以这是一个射影变换． (PP′Q′R)＝(PP′R′Q) (PP′Q′R)＝(P′PQR′) 根据定理2．4知这射影变换是一个对合．
如图2—3—11．直线l与完全四点形ABCD的三对对边的交点为P,P′；Q,(C)Q′；R,R′．在l上P→P′,Q→Q′,R→R′,因为(P,P′,Q′,R)(P,E,A,B)(P,P′,R′,Q),所以这是一个射影变换．(PP′,Q′R)＝(PP′,R′Q)(PP′,Q′R)＝(P′P,QR′)根据定理2．4知,这射影变换是一个对合．
相似问题
设上题里的常数是2．两个自对应元素的参数是1 －1 求射影变换式．请帮忙给出正确答案和分析 谢谢！
设上题里的常数是2．两个自对应元素的参数是1，－1，求射影变换式．请帮忙给出正确答案和分析，谢谢！
设(P) (P′)是两个重叠的射影点列 R与R′是任一对应点 当无穷远点作为(P)中点时 其对应点是
设(P)、(P′)是两个重叠的射影点列，R与R′是任一对应点，当无穷远点作为(P)中点时，其对应点是A′，当无穷远点作为(P′)中的点时，其对应点是B，求证：A
已知直线l1 l2 l3 l4的方程分别为：2χ－y＋1＝0 3χ＋y－2＝0 7χ－y＝0 5χ－
已知直线l1，l2，l3，l4的方程分别为：2χ－y＋1＝0，3χ＋y－2＝0，7χ－y＝0，5χ－1＝0， 求证：四直线共点，并求(l1l2，l3l4)．请帮忙给出正确答案和分析，谢谢！
求二无穷远点cu12＋2huu＋bu22＝0在互相垂直的方向上的条件．请帮忙给出正确答案和分析 谢谢
求二无穷远点cu12＋2huu＋bu22＝0在互相垂直的方向上的条件．请帮忙给出正确答案和分析，谢谢！
求作下列图形的对偶图形． 写出下列命题的对偶命题 (1)两点决定一直线； (2)射影平面上写出下列命
求作下列图形的对偶图形． 写出下列命题的对偶命题 (1)两点决定一直线； (2)射影平面上写出下列命题的对偶命题 (1)两点决定一直线； (2)射影平面上
