设(P) (P′)是两个重叠的射影点列 R与R′是任一对应点 当无穷远点作为(P)中点时 其对应点是
设(P)、(P′)是两个重叠的射影点列，R与R′是任一对应点，当无穷远点作为(P)中点时，其对应点是A′，当无穷远点作为(P′)中的点时，其对应点是B，求证：A′R′.BR＝常数．
请帮忙给出正确答案和分析，谢谢！
参考解答
473***102
2024-11-20 00:20:43
正确答案：设R1→R′1R2→R′2是此射影对应下任二对对应点则由已知条件可得： (R1R2P∞B)
(R′1R′2A′P′∞) 故有(R1R2P∞B)＝(R′1R′2A′P′∞)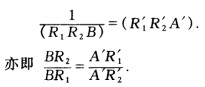 
所以A′R′1.BR1＝A′R′2.BR2＝常数．
设R1→R′1,R2→R′2是此射影对应下任二对对应点,则由已知条件可得：(R1,R2,P∞,B)(R′1,R′2,A′,P′∞),故有(R1R2,P∞B)＝(R′1R′2,A′P′∞),所以A′,R′1.BR1＝A′R′2.BR2＝常数．
相似问题
已知直线l1 l2 l3 l4的方程分别为：2χ－y＋1＝0 3χ＋y－2＝0 7χ－y＝0 5χ－
已知直线l1，l2，l3，l4的方程分别为：2χ－y＋1＝0，3χ＋y－2＝0，7χ－y＝0，5χ－1＝0， 求证：四直线共点，并求(l1l2，l3l4)．请帮忙给出正确答案和分析，谢谢！
求二无穷远点cu12＋2huu＋bu22＝0在互相垂直的方向上的条件．请帮忙给出正确答案和分析 谢谢
求二无穷远点cu12＋2huu＋bu22＝0在互相垂直的方向上的条件．请帮忙给出正确答案和分析，谢谢！
求作下列图形的对偶图形． 写出下列命题的对偶命题 (1)两点决定一直线； (2)射影平面上写出下列命
求作下列图形的对偶图形． 写出下列命题的对偶命题 (1)两点决定一直线； (2)射影平面上写出下列命题的对偶命题 (1)两点决定一直线； (2)射影平面上
写出图1—2—14的点线结合关系 说出其对偶命题 并画出对偶图形． 请帮忙给出正确答案和分析 谢谢！
写出图1—2—14的点线结合关系，说出其对偶命题，并画出对偶图形． 请帮忙给出正确答案和分析，谢谢！
已知射影坐标变换式：设直线l上以2 4为坐标的点及无穷远点顺次对应直线l′上以－1 1为坐标的点及无
已知射影坐标变换式：设直线l上以2，4为坐标的点及无穷远点顺次对应直线l′上以－1，1为坐标的点及无设直线l上以2，4为坐标的点及无穷远点顺次对应直线l
